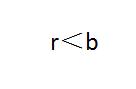分割后的数字相加,若结果能整除37,则原数也能整除它
以上是几个对10的整数幂同余±1的几个质数,整除规则相对简单。很多质数对10的整数幂同余不是±1的怎么判断呢?我们就以17举例:17*6=102,对100余数是-2,这个就比较麻烦了,因为按照同余定理,需要对每两位分割的数字乘以2的对应次幂再加减,如果M有很多位,这个方法将不具有可行性。

分割后的数字要乘以2的次幂再进行加减,比以上那些数麻烦很多,如果原数有很多位,这种方法就没有可行性。
我们的解决方案就是截尾法。假设M的尾数为b,剩下的数字为a,则M=10a b,截尾法就是依据同余定理,将a的系数化为1。也就是把N位数的M,转换为N-1位的Q
下面以17为例,如果10a b能够被17整除,那么5(10a b)也可以被17整除,而5(10a b)=50a 5b=51a-a 5b=51a-(a-5b),51=3*17可以整除17,因此,M=10a b与a-5b对17同余,M是否整除17相当于a-5b是否整除17。也就是截断M的尾数后,还要减去尾数的5倍,如果结果能被17整除,那么原数就能被17整除。如此继续进行,直到结果能够容易判断为止。
其他质数也是类似,目的就是将a的系数简化为1,具体算法的C#代码和注释描述如下:
static int GetPrimeRuleParam(int prime)
{
switch(prime % 10)
{
case 3: return (1 prime*3)/10;//尾数为3,该数的三倍加一再除以10
//13->4,23->7,43->13,53->16,73->22,83->25
case 9: return (1 prime)/10;//尾数为9,该数加一再除以10
//19->2,29->3,59->6,79->8,89->9
case 7: return (1-prime*3)/10;//尾数为7,用一减去该数的三倍再除以10
//7->-2, 17->-5, 37->-11, 47->-14, 67->-20, 97->-29
case 1: return (1-prime)/10;//尾数为1,用一减去该数再除以10
//11->-1,31->-3,41->-4,61->-6,71->-7
default: return 0;//尾数为其他,不是质数,返回0
}
}