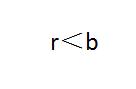1.整数a除以整数b(b≠0),商是整数而没有余数,我们就说a能被b整除,b能整除a。
2.a与b的和除以c的余数,等于a、b分别除以c的余数之和除以c的余数。
3.a与b的乘积除以c的余数,等于a、b分别除以c的余数的积除以c的余数。
4.若两个数a、b除以同一个数m得到的余数相同,则a、b的差一定能被m整除。
5所谓同余问题,就是给出“一个数除以几个不同的数”的余数,反求这个数,称做同余问题。

精讲1:甲、乙两数的和是1088,甲数除以乙数得商11余32,求甲、乙两数。
分析: 解答这样的问题,首先要根据除法的意义,理顺被除数、除数、商和余数之间的关系,即被除数=商×除数 余数。
因为甲=乙×11 32,所以甲 乙=乙×11 32 乙=乙×12 32=1088。
解:乙=(1088-32)÷(11 1)=88 甲=1088-88=1000
精讲2:求478×296×351除以17的余数。
分析:先求出乘积再求余数,计算量较大,可以根据同余定理“a与b的乘积除以c的余数,等于a,b分别除以c的余数的积除以c的余数”,先分别计算出各因数除以17的余数,再求出余数之积除以17的余数。
解:478÷17=28······2
296÷17=17······7
351÷17=20······11
2×7×11÷17=9······1
精讲3:有一个大于1的整数,除45、59、101所得的余数相同,求这个数。
分析:根据同余定理“若两个数a、b除以同一个数m得到的余数相同,则a、b的差一定能被m整除”, 我们可以得到:这个数一定能整除这三个数中任意两数的差,也就是说它是任意两数差的公约数。
解:101-45=56 59-45=14 (56,14)=14
14的约数有1、2、7、14,所以这个数可能为2、7、14。
精讲4:2001年的国庆节是星期一,求2010年的国庆节是星期几?
分析:一个星期有七天,要求2010年的国庆节是星期几,只要求从2001年国庆节到2010年国庆节的总天数被7除的余数就行了。2001年国庆节到2010年国庆节之间共有2个闰年、7个平年,即有366×2 365×7天,如果我们利用同余性质“a与b的和除以c的余数,等于a,b分别除以c的余数的和除以c的余数”,就可以不必算出这个总天数。
解:366×2÷7的余数是4,365×7÷7的余数是0,
(366×2 365×7)÷7的余数是4 0=4. 1 4=5
答:2010年的国庆节是星期五。
精讲5:学校新买来118个乒乓球,67个乒乓球拍和33个乒乓球网,如果将这三种物品平均分给每个班级,那么这三种物品剩下的数量相同,请问学校共有多少个班?
分析:所求班级数是除118,67,33余数相同的数,那么可知该数应该为118-67=51和67-33=34的公约数,(51,34)=17。
答:学校共有17个班。