高中刚接触自然对数的底数 e 时就觉得这货很奇怪。e≈2.71828…,是一个无理数,很多人都不禁要问它为什么约等于 2.71828…,这其中有什么深层的原理吗,e 的神奇之处,现在我们就来简单聊聊……
e的神奇可以从复利说起。复利是一种利息的计算方法,在存钱时把上期末的本利和作为下一期的本金,又计入下一期计算利息。比如一个银行的年利率是 50%(目前还没这种银行),存100元钱,一年后的本利和是 150 元;存两年按复利计算的本利和是 元。现在假设有一个银行,它的年利率是 100%(这种银行更不存在),我们存入 1 元钱,一年后的本利和是2元。我们知道存一年本利和是本金的(1 1)=2倍,则存半年效果是本利和变成本金的倍,所以若银行每半年付利息,我们可以把利息马上存入,1年末的本利和是元,存4个月效果是本利和变成本金的倍,所以若银行每4个月就付利息,利息生利息,年底的本利和是元。

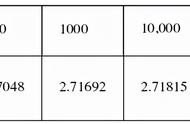
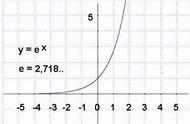
一年365 天,若银行愿意天天付利息,这样利滚利的余额2.71456748202元,假设银行丧心病狂的每秒付利息,你也丧心病狂的每秒都再存入,1年共31536000 秒,利滚利的余额2.7182817813元。所以能够发现,1元钱存1年,在年利率 100% 情况下,无论怎么利滚利,其余额总有一个无法突破的天花板,这个天花板就是e≈2.71828…。用极限语言描述就是:

所以,这样存钱即使累死也没多挣几个钱。

我们把自然增长率的极限称为e,即在年利率 100% 情况下,存钱的最高本利和就是本金的e(约为2.71828…)倍。
那自然对数又是怎么回事呢?
我们先从一个虚构的故事说起:有一土豪要去银行存款,比如存10万元。银行经理推荐他投资理财产品,说有很高的年利率,然后说按照指数运算方法……,银行经理巴拉巴拉讲了一通。但土豪的数学只有小学水平,听不懂有点烦,就问投资多长时间能有一成收益,两成收益,翻倍的收益?经理有点懵,这土豪不按常理出牌!一般人都是根据存款时间问收益,例如收益第 1 年多少、第 2 年多少、第 3 年多少..... 土豪居然逆向思维,根据收益问时间,多少年一成,多少年2成,多少年翻倍!不愧是老板,不问过程,只问结果!于是经理就从第 1 年开始算,把 10 年内每年的收益都算出来,列成一个收益列表然后再找出收益最接近一成,两成,及翻倍的年份指给土豪,土豪一看第 4 年、第 7 年、第 10 年就大概超过预期收益,非常高兴!经理用这张表查找收益,再找到最接近收益的大体年份的过程,其实就是指数运算的逆运算,是最简单的对数运算,这个表就是对数表的简洁形式。
为了认识对数概念,我们再来看看《人教版新课标高中数学A版必修1》第二章 2.2 对数函数小节课后阅读材料《对数的发明》: