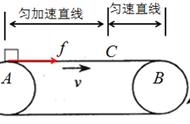
【题文】如图所示,质量 的长木板Q静止在光滑水平面上,右端紧靠光滑固定曲面AB的最低点B,木板上表面与曲面相切于B,水平面的左侧与木板左端相距为x(未知且可调)处有一挡板C。一质量 的小滑块P(可视为质点)从曲面上与B的高度差为1.8m处由静止滑下,经B点后滑上木板,最终滑块未滑离木板。已知重力加速度大小为 ,滑块与木板之间的动摩擦因数为0.3,木板与左挡板C和最低点B的碰撞中没有机械能损失且碰撞时间极短可忽略,则从滑块滑上木板到二者最终都静止的过程中
(1)若木板只与C发生了一次碰撞,求木板的运动时间;
(2)若木板只与C发生了二次碰撞,求最终P与B点的距离;
(3)若木板只与C发生了三次碰撞,求x的值;
(4)其他条件不变,若m=2kg 、M=1kg ,,求木板通过的总路程。

【相关考点】
第一个知识点是动能定理。主要涉及到第(1)问;
第二个知识点是滑块木板的动量问题。这个知识点是这个题的核心知识点,涉及整个题的分析。滑块木板在光滑水平面、并且无外力的情况下是一定可以使用动量守恒定律的,这是滑块木板的动量问题的基础;
第三个知识点是滑块与木板碰撞的次数分析。这个知识点是这个题能不能拿分的一个关键知识点,重点在于什么情况下木板才会只和挡板C发生几次碰撞。
第四个知识点是往返运动求总路程的问题。这个知识点是这个题难度最大的一个考点,它不是动能定理方面的往返运动求总路程的内容,而是这个题中需要我们对整个运动过程进行分析,整理清楚滑块与木板的运动过程,才能将这个题做出来。
【难度分析】
这个题的难度比较大。如果知道木板与挡板C什么情况下只会发生一次碰撞的话,能比较容易地将第(1)问做出。但是从第(2)问开始,难度都已经提高到一个比较难的程度了。
不过如果能将这个题理解清楚,对于滑块木板的动量问题这一类型,会有很大的帮助。这是滑块木板比较压轴的一种题型。
这个题重在分析过程,也就是木板在数次与挡板碰撞的过程中,滑块木板分别会怎么运动,以及它们之间的相对关系是什么样的。这些内容主要考查同学们的分析问题的能力、检验同学们的逻辑思维能力。
【思路分析】
想要分析清楚这个题,我们的重点是要分析清楚在什么情况下,木板才只会与挡板C发生一次碰撞;什么情况下木板会与挡板只发生二次碰撞,或者只发生三次碰撞。
很多同学会以为只要滑块与木板能够共速,则滑块与木板才只会发生一次碰撞,这其实是不对的。我以前教的学生中,有很多同学都是这么认为的。
那关于这个内容,到底什么条件才是正确的呢?现在我们就一起来分析分析。
在木板与挡板C和最低点B碰撞之后,木板的速度会大小不变,方向反向。如果在木板第一次与挡板C发生碰撞之前,滑块已经与木板共速,因为木板的质量大于滑块的质量,则碰撞之后,木板的动量会大于滑块的动量,滑块与木板会再次共速然后与最低点B发生碰撞。
木板与最低点B发生碰撞之后,木板的速度又会反向。又因为木板的质量大于滑块的质量,所以木板的动量会大于滑块的动量,滑块与木板又会再次共速然后与挡板C发生第二次碰撞。然后一直反反复复下去。
当然,如果滑块与木板是这样运动的话,木板与挡板C之间不可能只发生一次碰撞,也不可能只发生二次碰撞或者只发生三次碰撞。理论上,木板与挡板C会一直碰撞下去。
所以在这个题中,滑块与木板是不可能共速的。我们需要再对它进行分析,找到滑块与木板符合题意的运动方式才行。
(1)想要木板与挡板C只发生一次碰撞,则在木板与挡板C第一次碰撞的瞬间,滑块与木板的动量必须要大小相等才行,即,如下图所示。当木板与挡板C第一次碰撞之后,木板的动量大小不变,方向反向。就会造成第一次碰撞之后滑块的动量就和木板的动量大小相等、方向相反,滑块和木板的速度会同时减到0,木板就不会再和挡板C发生第二次碰撞,则只会发生一次碰撞。

现在我们先用动能定理求出滑块运动到B点时的速度大小,这个动能定理式子为,经计算可得。
当滑块滑上木板之后,因为水平面光滑并且无外力作用,所以滑块与木板一定满足动量守恒的条件。对滑块和木板使用动量守恒定律得,再结合式子,我们就可以求出木板与挡板C第一次碰撞之后的速度大小分别为、。
整个过程中,木板受到的滑动摩擦力保持不变,所以木板的加速度也保持不变。木板的牛顿第二定律的式子为,求得木板的加速度大小为。
所以木板先是以加速度向左做匀加速直线运动,接着以 的速度撞击挡板C,然后再以的速度反向做加速度为的匀减速直线运动,直到速度减为0。
因为匀变速直线运动的对称性,木板向左做匀加速直线运动和向右做匀减速直线运动的时间相等,所以整个过程中,木板运动的总时间等于木板向左做匀加速直线运动的时间的2倍,即。
如果想要木板与挡板C至少发生一次碰撞,只需要满足在木板与挡板C第一次碰撞的瞬间,滑块的动量大于等于木板的动量,即。
(2)分析清楚了木板与挡板C只发生一次碰撞的条件之后,现在来分析木板与挡板C只发生二次碰撞的条件就轻松多了。想要木板与挡板C只发生二次碰撞,只要在木板与挡板C第二次碰撞的瞬间,滑块与木板的动量大小相等就行,即。

但是想要求出第(2)问,没有那么麻烦,因为在第(2)问中求的是最终滑块P与B点的距离的大小。我们对滑块P进行受力分析会发现,不管木板与挡板C发现几次碰撞,滑块P一直在向左做匀减速直线运动,直到最终滑块P的速度减为0。滑块P的加速度大小由牛顿第二定律计算为。
我们现在对滑块P用运动学公式就可以求出最终滑块P与B点的距离,这个运动学公式为。经计算,我们便可求出最终滑块P与B点的距离大小为。
现在我们来分析第(3)问。根据对第(2)问的分析过程可知,在第(3)问中,想要木板只与挡板C发生三次碰撞,则只要在木板与挡板C第三次碰撞的瞬间,滑块与木板的动量大小相等就行,即。
而想要更顺利地解决第(3)问,我们还需要对木板的运动有一个更深层次地分析才行。在第(1)问中,我们已经分析出木板向左匀加速运动和向右交减速运动的加速度的大小都为,所以木板向左做匀加速直线运动和向右做匀减速直线运动具有对称性。
这个更深层次地分析结果就是当木板每次向右做匀减速运动到速度为0时,木板的右端刚好与B点接触。从这个角度进行分析可知,木板每次与挡板C碰撞的速度大小都相等。
所以木板的完整的运动过程如下所示:木板从静止开始以加速度向左做匀加速直线运动,接着以速度撞击挡板C,然后再以该速度向右做加速度为的匀减速直线运动。当木板的速度减为0时,木板的右端刚好与B点接触。然后又从静止开始向左做匀加速运动,以速度与挡板碰撞之后再向右做匀减速运动,如此循环往复,直到第三次与挡板C碰撞之后,向右匀减速运动直到速度减为0。
所以木板左端到挡板C的距离可以直接使用运动学公式求出,只不过现在还需要求出的大小。
假设木板第一次与挡板碰撞时,滑块P的速度大小为;第二次与挡板碰撞时,滑块P的速度大小为。则:
从滑块P滑上木板到木板第一次与挡板C相撞的过程中,动量守恒定律式子为;
从木板第一次与挡板C碰撞之后的瞬间到木板第二次与挡板C碰撞之前的瞬间的过程中,动量守恒定律式子为;
从木板第二次与挡板C碰撞之后的瞬间到木板第三次与挡板C碰撞之前的瞬间的过程中,动量守恒定律式子为;
又因为,所以结合这四个式子,我们就可以求出木板与挡板C碰撞时的速度。
现在我们已经求出了的大小,就可以使用运动学公式求出木板左端到挡板C的距离的大小为。
现在我们开始分析最后一问,也是这个题的压轴问题。如果其他条件不变,但是、,,求木板通过的总路程。
现在虽然条件变了,但是总体分析思路一点都没有改变。理解清楚了这种题型的思路,对于这种题型就没有必要惊慌。所谓家里有粮,心中不慌。
首先第一个问题是木板第一次与挡板C碰撞之前,滑块与木板有没有达到共速。分析方式自然是求出木板一直加速到与挡板C相撞时的速度,将这个速度和滑块与木板的共同速度做比较。
木板在运动过程中的加速度的大小由牛顿第二定律求出得。如果木板一直做左做匀加速直线运动,则木板第一次与挡板C相撞时的速度大小由运动学公式求出为。
对滑块和木板使用动量守恒定律得,滑块与木板的共同速度大小为。因为,所以当滑块与木板刚好共速时,木板与挡板C发生第一次碰撞。
木板与挡板C第一次碰撞之后,木板原速反弹。在木板与挡板C第二次碰撞之前,如果滑块与木板不会共速的话,木板仍会以速度撞击挡板C。但是根据动量守恒定律,在木板与挡板C第二次碰撞之前,滑块与木板的共同速度大小,所以木板第二次与挡板C碰撞之前,滑块与木板已经共速。
从上方的分析得知,在木板与挡板第一次碰撞之后的每一次碰撞之前,滑块与木板都能达到共速。并且木板与挡板C相撞时的速度大小都等于前一次与挡板C碰撞时的速度的。
木板第一次与挡板C碰撞之前的路程大小为,并且;
因为木板与挡板C碰撞之后会原速反弹,所以木板第一次与挡板C碰撞之后到第二次与挡板C碰撞之前的路程大小为;
从木板与挡板C第二次碰撞开始,木板与挡板C相撞时的速度大小都等于前一次与挡板C碰撞时的速度的。根据运动学公式可知,从第二次碰撞开始,木板每两次与挡板C相撞的时间间隔内,木板的路程都是前一段时间间隔内的路程的。
所以木板第二次与挡板C碰撞之后到第三次与挡板C碰撞之前的路程大小为;
木板第三次与挡板C碰撞之后到第四次与挡板C碰撞之前的路程大小为;
木板第四次与挡板C碰撞之后到第五次与挡板C碰撞之前的路程大小为;
以此类推…………
木板第n-1次与挡板C碰撞之后到第n次与挡板C碰撞之前的路程大小为;
所以木板通过的总路程的大小为,即。根据等比数列求和公式,我们可以求出木板的总路程为。
当时,。
,