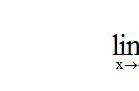函数的连续性是数学分析中一个重要的概念,它描述了函数在某一点处的变化情况。
如果一个函数在某一点处没有间断,则称该函数在该点处是连续的。
在函数连续性的基础上,我们可以推导出许多重要的数学定理和结论,因此函数的连续性在数学领域中具有重要的应用价值。
为了更好地理解函数的连续性,我们可以先从它的定义入手。
函数的连续性定义如下:
设函数f(x)在点x=a的某个邻域内有定义,如果当x→a时,函数f(x)的极限为f(a),则称f(x)在点x=a处连续。
这个定义可以简单理解为:函数在某一点处连续,当且仅当该点的函数值等于其极限值。
那么,如何判断一个函数是否连续呢?我们可以通过以下三个步骤来进行判断:
第一步:观察函数在某一点处是否具有定义。如果函数在该点处没有定义,那么该函数在该点处一定是间断的。
第二步:观察函数在某一点处的极限是否存在。如果函数的极限存在,那么该函数在该点处的极限等于其函数值。
第三步:观察函数在某一点处的左右极限是否存在且相等。如果函数的左右极限存在且相等,那么该函数在该点处是连续的。
下面我们来看一个例子:
设函数f(x) = x²在区间[0, 2]上定义。显然,当x=0时,f(x)=0。
现在我们要判断f(x)在点x=2处是否连续。
第一步:显然,f(x)在点x=2处有定义,f(2)=4。
第二步:当x→2时,f(x)的极限为f(2)=4,因此f(x)在点x=2处的极限等于其函数值。
第三步:由于f(x)在点x=2处的左右极限都存在且相等,因此f(x)在点x=2处是连续的。
综上所述,我们可以得出结论:函数f(x)=x²在区间[0, 2]上是连续的。
函数的连续性是数学分析中的一个重要概念,它为我们研究函数的性质提供了基础。
通过对函数连续性的理解,我们可以更好地把握函数的性质,从而为解决实际问题提供帮助。