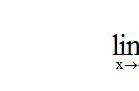不知道大家听没听过一首儿歌,叫做《蜗牛与黄鹂鸟》。你要知道蜗牛是“一步一步爬上去”的,无论我是以一年四季为单位还是以分秒为单位,它都是连续的向上爬的。为啥今天我要给大家提这么一首歌呢?原因就在于我要利用这个给大家聊聊函数的连续性。你想,我在说蜗牛连续向上爬的时候,提到一句话,就是我无论怎么放大研究它都是连续的。看图:

无论我把时间怎么拉长,蜗牛的路线都是连续的,(我画成了指数函数是随手一画的,无论什么函数都是这样)。

不要觉得我画的x和y的增量太大,记住导数有的时候要把它视作是一种放大图来理解。什么意思?就是你看上去很大,那是经过放大的,你可以认为它很小。接下来,我们尝试着给连续性下一个定义:就是有这么一个函数,我无论让它的横坐标怎么拉长,都是一条连续的线段,换句话说,就是x变化很小那么y也变化很小。大家知道,这么说还不够准确,那么究竟什么才是准确的呢?

你应该理解吧,这个就是我刚刚说的那些的数学表达,对吧!先保证有定义,之后在保证x变化很小的时候,y的变化也不会大。再看第二个:

不小心笔误了,应该为x→x0。
虽然是两个定义,说的却是一回事。都是在强调x与y在一段很小的区间里变化都不会太大。第一个不用说了,第二个就是在f(x0)附近求极限看看它是怎么变化的,结果这个函数就是无限的向f(x0)靠拢,Δx越小(x距离x0越近),那么y也越接近f(x0),当x=x0的时候,y=y0了。(你自己要画个图来琢磨,一味地看是不管用的)。
最后一个其实就是用ε-Ν语言把这些话重新说一遍:

话说到这,我们应该对函数连续的定义有一个准确的理解了。那你想想,函数的连续性与可导有没有什么联系呢?
你想一下,连续只是在提函数连续不断,而导数呢?它说的是,我在这一点可以指引函数下一点怎么走。所以说,函数不连续,求导就无从谈起。那就是说可导的函数必定连续。
可是连续的函数不一定就可导哦!因为有的函数它在某点不可导(例如y=|x|),还有的函数它有切线但是斜率不存在(与x轴相垂直)。

今天就和大家说这么多了,谢谢大家!