例题:在三棱锥P-ABC中,PA⊥平面ABC,AB=2,BC=3,PA=4,∠ABC=,则该三棱锥的外接球的体积为:( )
分析:一开始以为该三棱锥存在共斜边的两个直角三角形,那样就可以大大减少计算量了。于是根据题中给出的条件,利用勾股定理,余弦定理算出PB、AC、PC的长度,但是PB、AC、PC三边构成的三角形不是直角三角形,共斜边直角三角形方法不适用,马上转变思路。
根据球心的定义来计算吧。
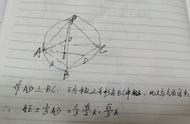
过球心O和P点做出该外接球的截面,为了便于观察,不画完整的三棱锥,仅把P点、A点和三角形ABC所在的外接圆画出来,连接OP、OA,因为P、A、B、C都在同一球面上(外接球),所以OP=OA,过O点作AP的垂线,交于D,则D为A的中点.
三角形ABC的外接圆的半径,根据正弦定理可以求出.在三角形ODA中,利用勾股定理,即可求出球心半径R.