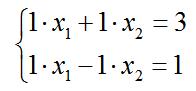许多同学学习线性代数这门课,都是从行列式开始的。半本教材学完了,还在懵逼中:这线性代数究竟讲的是啥?
不怪同学们不努力,只因教材有问题,行列式本身太过抽象,作为线性代数入门第一课实在有些不合适。
那么如何让线性代数这门课形象起来呢?让我们从一个最简单的二元一次方程组开始,由它的几何意义,切入线性代数这门课。
看下面的二元一次方程组:

答案一目了然,x=2,y=1。我们知道,求解一个二元一次方程组,除了代数运算外,用函数曲线的方法也可以,画图即可求解。
那么,我们把这个二元一次方程组变换一下形式:
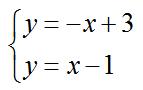
在平面坐标系中(二维平面),画出两条函数曲线(当然很明显这是两条“直线”),如下图:

从图中可以看出,二元一次方程组的解,与两条函数直线的交点是等价的。
我们将这个结论拓展一下,从二元一次方程组拓展到三元一次、四元一次直至N元一次方程组。如果它们各自有解,就可以说,在三维、四维直至N维坐标系中,方程组中全部方程所代表的函数直线,在相应的坐标系内有唯一交点。
但是,问题来了,不管它们有没有解,一旦未知元数超过3个,图画不出来啊,谁也没见过四维空间长啥样不是?而且,方程组中的一个方程式并不只对应一条函数直线,也可能是无穷多条直线。
另外,求解N元一次方程组,代数运算更不现实,计算量得多大呀。
好啦,到这里,我们已经站在线性代数的起点上了,那就是如何处理上述函数直线的关系。
该如何处理呢?答案是------不处理!因为我们要重塑上述的函数图形。
在重塑上述的函数图形之前,我们先重塑上面的二元一次方程组,将其变成下面这样的形式: