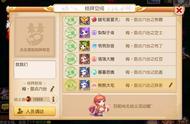
- (a)在量子理论中,引力量子称为引力子,用h表示。引力通过分解黎曼度规张量而构成。在这种理论中,物质通过交换这种引力包而相互作用。以这种方式,我们完全失去了爱因斯坦美丽的几何绘景。(b)不幸的是,所有圈图都是无穷大,这在过去半个世纪中阻碍了引力与量子理论的统一。
图中,我们看到两个中性粒子交换一个引力量了,它用场h来标记。当我们将所有的圈图求和时,问题就出现了。我们发现它们是发散的,就像图中(b)那样。对于杨-米尔斯场,我们能用一些技巧,使这些无穷大量或者渐渐消除,或者被吸收到某个不可测量的量中。然而,可以证明,把它们用于量子引力理论时,我们发现通常的重正化步骤完全失效了。
80年代初,一种奇妙的现象出现了。物理学家们开始克服对不可见维和超空间的偏见,准备采用某种替代方案,那就是卡鲁查-克莱因理论。
虽然卡鲁查-克莱因理论仍然不可重正化,但它提供了用大理石构造某种理论的希望。但是在20世纪30年代和40年代,人们对物质(爱因斯坦称他场方程中的物质为“丑陋的木头”)的本质几乎一无所知。然而,到了70年代,标准模型终于解开了木头的奥秘∶物质由遵循SU(3)×SU(2)xU(1)对称性的杨-米尔斯场结合在一起的夸克和轻子所组成。问题是如何从几何(爱因斯坦称之为美丽的大理石)导出这些粒子和神秘的对称性。
这似乎是不可能的。毕竟,这些对称性是点粒子之间互相交换的结果。如果一个多重态中的N个夸克彼此打乱后*,那么对称性就是SU(N)。这些对称性似乎是木头独有的对称性,而不是大理石的对称性。SU(N)与儿何学又有什么关系呢?
把木头变成大理石
60年代出现了第一条小小的线索。物理学家们发现了另一种把对称性引进物理学中的方法。当物理学家们把旧的(五维)卡鲁查-克莱因理论扩展到N维时,他们意识到存在着将某种对称性施予超空间的自由。在第五维被卷曲起来时,他们看到麦克斯韦场跳出了黎曼度规。但是当N维被卷曲起来时,物理学家们发现著名的杨-米尔斯场(标准模型的关键)从他们的方程中跳了出来。
为了弄明白对称性怎样从空间出现,考虑一个普通的浮水气球。它有一种对称性∶我们能把它绕自己的中心旋转,浮水气球仍保持它原有的形状。浮水气球的对称性,或者球的对称性,称为O(3)对称性。类似地,在更高的维中,也能让一个超球绕它的中心旋转,且保持其形状不变。这个超球所具有的对称性称为O(N)。
如果我们以某种确定的方式振动浮水气球,那么我们就能在球面上诱导出规则的振动,这种振动称为共振。这些共振只能以某些确定的频率振动。如果使浮水气球振动得足够快,那么就能产生某个确定频率的声调。这些振动又可由O(3)对称性来分类。
像浮水气球一样,膜也能诱导共振频率。例如,我们喉部的声带是一些被拉伸的膜,这些膜以确定的频率振动,或者说共振,因此能产生声调。对于超球而言,效果也是这样。它也像膜那样可以以各种频率共振,这些振动又可由它的O(N)对称性所确定。另一方面,数学家们早已设想用复数来描述高维中的更微妙复杂的表面,相应于复"超球"的对称性是SU(N)。
现在关键在于∶如果一个粒子的波函数沿着这个表面振动,那么它就将继承这种SU(N)对称性。这样,在亚原子物理学中出现的这种神秘的对称性SU(N),现在就可以看作超空间振动的副产品。换句话说,物质的对称性的起源有了一种解释∶它们确实是来源于几何的对称性。
现在,我们如果取一种定义在4+N维中的卡鲁查-克莱因理论,然后把N维卷曲起来,我们就发现方程分成了两块。第一块是通常的爱因斯坦方程,这是我们希望找到的。但第二块却不是麦克斯韦理论。我们发现,余下的正好就是杨-米尔斯场,它是所有亚原子物理学的基础。这是把木头对称性转变成大理石对称性的关键所在。
起初,物质对称性自动从高维中显现出来仿佛很不可思议。物质对称性是通过检验从原子对撞机中产生的废料而被发现的。极难想象,通过将夸克和轻子打乱*而发现的对称性应该起源于超空间。有一种类比也许有助于我们理解这一点。物质也许可以比作没有形状和凹凸不平的粘土,它缺乏几何图案固有的美丽的对称性。然而,粘土可以被压成模具,模具则可以有对称性。这样,粘土也就继承了模具的对称性。粘土(像是物质)继承了它的对称性,是因为模具(像是时空)具有对称性。
如果这正确的话,那就意味着我们在夸克和轻子之间看到的奇特的对称性现在可以看作超空间中振动的副产品。例如,如果那些看不见的维有SU(5)对称性,那么我们就能把SU(5)大统一理论写成某种卡鲁查-克莱因理论。
这也能从黎曼度规张量中看到。我们想起黎曼度规张量除了有更多的分量以外,很类似于法拉第场。把方格棋盘中的第五列和第五行分出,我们就能将麦克斯韦场与爱因斯坦场分开来。现在,在(4+N)维空间中实施与卡鲁查-克莱因理论同样的做法。如果把这 N行和N列与前面四行和四列分离开来,那么将获得既描述爱因斯坦理论也描述杨-米尔斯理论的度规张量。

如图所示,我们已经刻画出一个(4+N)维卡鲁查-克莱因理论的度规张量,图中已把爱因斯坦场与杨-米尔斯场分离开来。
从事量子引力研究的物理学家德威特是最先实施这种做法的物理学家之一。一旦找到了分解度规张量的诀窍,抽出杨-米尔斯场的计算就很简单了。德威特觉得从N维引力理论中分离杨-米尔斯场在数学上如此简单,以至于在1963年法国的一次夏季物理学研讨班上,他竟将它作为一道家庭作业布置下去。
把杨-米尔斯场从卡鲁查-克莱因理论中提取出来还只是第一步。虽然物质的对称性现在可以看作源于看不见的维中的隐藏的对称性,下一步却是完全由几何来创造(由夸克和轻子构成的)物质本身。
超引力
把物质转变成几何,仍然面临着一些棘手的问题。因为,根据标准模型,所有的粒子都在“自旋”。例如,我们现在知道物质由夸克和轻子构成。夸克和轻了都具有1/2个量子自旋单位(以普朗克常量h为测量单位)。具有半整数自旋(1/2,3/2,5/2等)的粒子被称为费米子。然而,力由具有整数自旋的量子来描述。例光子具有1个自旋单位。杨-米尔斯场亦是如此。假想的引力子,则具有2个自旋单位。它们称为玻色了。
传统上,量子理论使费米子和玻色子严格分开。把物质转变为几何的任何努力,都将不可避免地面对这一事实∶玻色子和费米子是性质不同的两个世界。例如,SU(N)可以把夸克打乱后*,但费米子和玻色子却决不允许彼此相混。因此,当人们发现被称为超对称的新的对称性时,使人震惊的是它确实把玻色子和费米子混起来了。超对称的方程允许一个玻色子和一个费米子相交换而仍然保持方程的原貌。换句话说,一个超对称的多重态包含有相等数目的玻色子和费米子。在同一多重态内打乱并*玻色子和费米子,超对称方程仍保持原样。
这给了我们一种把宇宙中所有粒子放进一个多重态的可能性。像诺贝尔奖得主萨拉姆所强调的那样,
超对称是所有粒子完全统一的最终方案。
超对称以一种新型的数字系统为基础,显然正确的大多数乘除运算对超对称是无效的。例如,如果a和b是两个“超数”,那么a×b=-b×a。
当然,这对普通的数而言是绝对不可能的。因为,如果a×a=-a×a,那么a×a=0。如果这些数是普通的数,那么这将意味着a=0,数的系统就此崩溃了。
然而,由于是超数,因此数的系统并不会崩溃,有一种相当惊人的说法,那就是甚至a≠0,也可以有axa=0。虽然这些超数违背了我们学到的有关数的几乎一切知识,但是可以证明,它们产生了某种自洽而非常不平凡的系统。显然,可以以它们为基础建立一种全新的超级算法系统。
3位物理学家,弗里德曼、费拉拉和范尼乌文赫伊于1976年建立了超引力理论。超引力理论是构造一个完全由“大理石”组成的世界的首次实际尝试。在超对称理论中,所有的粒子都有超配偶子,它们被称为超粒子。弗里德曼的超引力理论只包含两种场∶自旋为2的引力子场(它是一个玻色子)及其自旋为3/2的配偶子,后者被称为引力微子。因为这些粒子还不足以把标准模型包括进来,人们又尝试把这一理论与更复杂的粒子匹配起来。
将物质包含在内的最简单的办法,是在11维空间中建立超引力理论。为了在11维中建立超卡鲁查-克莱因理论,人们必须大大增加黎曼张量中的分量,现在它就变成了超黎曼张量。为了理解超引力如何把木头转变成大理石,让我们写出度规张量,并说明超引力如何设法把爱因斯坦场、杨-米尔斯场以及物质场都装进一个超引力场。这个图的基本特点是,物质以及杨-米尔斯方程和爱因斯坦方程现在包容在同一个11维的超引力场中。

- 超引力几乎圆了爱因斯坦的梦,这个梦就是用纯几何学导出宇宙中所有的力和粒子。为了理解这一点,注意如果我们把超对称性加进黎曼度规张量中,那么该度规的大小就翻了一番,从而给出了超黎曼度规。超黎曼张量的新分量相应于夸克和轻子。通过把超黎曼张量分解成它的分量,我们发现它几乎包含了自然界中所有的基本粒子和力∶爱因斯坦的引力理论,杨-米尔斯场和麦克斯韦场,以及夸克和轻子。但是在这个绘景中还缺失某些粒子,这一事实迫使我们走向某种更具威力的表述∶超弦理论。
超对称性是在超引力场中把物质转变成几何且反之亦然的对称性。于是,它们乃是同一种力的各种表现,这种力叫做超力。物质不再作为一种单一的孤立实体存在。它现在与几何合并而形成了超几何。