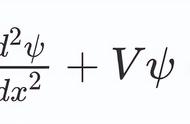而且你还要明白,求解出来的薛定谔方程的解不仅仅是一个函数,而且函数y是复数不是实数,实数我们都知道可以是1、2、1/3、根号2等等,但是复数可以是:1 3i(如果不懂啥时复数,可以去自己查查资料,这里就不解释),要表示一个复数,就必须用平面上的一个点,而不是数轴上的一个点,所以薛定谔方程的解,也就是波函数它的x是数轴上的一个点,但是y是一个平面上的点。由于y不是实数而是复数,所以这个解的函数图像就不太方面画出来,不过如果我们把y进行降维,只考虑实数上的的函数图像(也就是把真实的函数图像映射到实数平面上来)你会发现下图,其中x是一个粒子的位置,y的物理含义暂时不说。
其实由于我们的空间是三维的,刚刚的图只是二维,还有一个维度我们没用上,所以为了更直观的看到波函数的图像,我们可以把y依然保留再复数域,那么函数就是一个三维的图像,如下图所示,其中x依然是一个粒子的位置信息,y的含义还是暂时不说。

请注意这个图是一个三维的,所以你要把它当成一个三维图,不要在当成平面图来看,图像就好像是一圈一圈的环线一样围绕x轴旋转,中间部位比较胖,两端比较瘦。
这里要注意的是,薛定谔方程解出来的波函数,是一个与时间有关的函数,所以每一个时刻都有一个像上面一样的函数图,且每个时刻函数图都不一样。所以要完整的表达波函数,相当于要把每一个时刻的波函数图像画出来,然后把所有函数图串起来才是一个完整的波函数图像,如下图所示。

有了波函数我们能干啥呢?毫无疑问就是为了预测粒子的将来,就好像牛顿力学一样,我们可以根据平抛一个小球的初始信息,计算出将来任意一时刻小球的状态。但是由于微观世界具有不确定性,所以我们只能根据初始信息,计算出一个微观粒子将来某时刻“处于某种状态”的概率。所以波函数的作用就是用来求“概率”的。

刚刚上面所有的波函数的图像,其实是一个微观粒子的“位置波函数”图像,因为横坐标x是粒子的位置,如果把横坐标x换成粒子的速度,其实也能得出微观粒子的“速度波函数”图像,这个后面再谈。位置波函数自然就是用来预测一个微观粒子的位置信息。
当我们通过薛定谔方程,解出了一个位置波函数,那么t=1时,这个位置波函数就可以画出来,粒子处于任何可能的位置对应的概率值就都能求出来。当t=2时,这个位置波函数又会变成另外一幅图,粒子处于任何可能的位置对应的概率值又可以重新求出来。所以你要想知道未来粒子的状态,先明确到底要想知道哪个时刻的状态,然后把对应的位置波函数一画,粒子所有位置对应的概率都求出来了,这就是量子力学描述微观世界中一个粒子将来如何运动的方式。