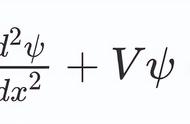我主要围绕微观世界的不确定性、叠加态等概念来讲解,其中主要讲解了爱因斯坦对微观世界的理解,以及哥本哈根学派对微观世界的解释。其实通过前面的文章我们可以看出,微观世界的确和我我们宏观世界差距非常大,由于人类几千年来都生活在宏观世界里,所以积累起来的经验和直觉一旦放到微观世界,我们就会觉得非常不可思议。但是诚如爱因斯坦提出狭义相对论时一个道理,也是一个非常反常识的理论,最后被证明居然是正确的,这也是人类第一次通过理性战胜直觉的巨大进步。

微观世界里面有几个奇特的现象,那就是微观世界具有“不确定性”,但是同时我们也知道不确定不等于不可研究,也不等于无规律,因为微观的“不确定”特点恰好就是微观世界的规律,所以我们只要掌握住了这个规律,一样可以研究微观世界来为人类服务,这个规律我们如何描述呢?那就是薛定谔方程。

可以这么说,牛顿定律在宏观世界里几乎是无所不能,那么“薛定谔方程”就是微观世界的“牛顿力学”,只不过微观世界一般人不会直接观看到,所以对薛定谔这个人感觉没有牛顿名气大,下面我正式给出薛定谔方程的形式。

咋看之下我相信大部分朋友都是直接蒙圈,这里面很多数学符号都很陌生,这和前面我给出爱因斯坦广义相对论“场方程”是一个效果,看后马上蒙圈。不过这里我还是要对比下,以前我写狭义相对论时,其实只要你懂速度公式v=s/t,其实任何人都是可以理解狭义相对论的。但是广义相对论和薛定谔方程,则不是一般人可以看懂,因为要理解这个方程,必须要学习高等数学,里面有很多概念比如“二阶”、“偏微分”、“非线性”、“拉普拉算符”、“定态”、“哈密顿量”、“复数”等等,陌生概念太多了,这里就不一一列举了,这里我也不打算多对每个陌生概念依次做解释,因为之前写广义相对论场方程时,已经不少网友表示枯燥无味,所以我直接解释这个方程是用来干啥即可。
首先你要明白薛定谔方程的解是一个“函数”,请注意我们以往解一个方程都是求出一个值,比如5x=20,我们可以算出解x=4。但是你要明白,薛定谔方程出来的解不是一个定值而是一个函数,函数就意味着说有x和y,一旦x值变化了,y值也要变化,比如函数y=x*2 3。