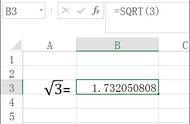
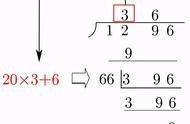
现在由于计算器的普及,手动开平方这项技能已经渐渐失传。但开平方是一种非常重要的运算,其难度远超四则运算和乘方。
《手动开平方》
小修(zck_math)
“我这儿有本秘籍。”

秘籍简介
《手动开平方》
打开秘籍看一看

《九章算术》中采用了数形结合的方法,
详细说明了开平方的方法、步骤。
根据几何上“出入相补”的原理,
“析理以词,解体用图”,
显示了中国传统数学的特色。
从几何上看开平方的运算,起源于“已知正方形的面积,求边长”的问题,需要借助于图形分割把平方根一位一位地开出来。
设正方形ABCD面积为361,
先估计√361的第1位数字因为
100<361<400
所以
10< √361<20
这说明√361的整数部分是二位数,
十位数字是1。

在AB上取AE = a = 10, 作小正方形AEFG,
其面积 ,SAEFG=100,
从大正方形中挖去小正方形AEFG,
余下一个直角的曲边形EBCDGF,面积为
SEBCDGF = SABCD - SAEFG = 361 -100= 261
再根据261确定√361的个位数。因为
SEBCDGF = SEBHF SGFID SFHCI= 2SEBHF SFHCI
设EB'=b, 则有
2ab b²=20b b²=(20 b)b
利用这个式子估计个位数, b分别取1, 2,…9,
取EB' = b = 9,
则 (20 b)b = 29 X 9 = 261
此时正好B'与B重合,开方开得尽。
所以√361= 19
如果B'与B不重合,还可以继续开下去。
我们试着来求常用的√2,假设正方形面积为2。

取AE = a = 1,
SEBCDGF = SABCD - SAEFG = 2-1= 1。
取EB' = 0.4
(2 b)b = 2.4×0.4 = 0.96,
1-0.96=0.04,
B'与B不重合,继续开
取B'B' '=0.01
2.81×0.01=0.00281。
再去B''B'''=0.004
…
可以得到√2≈1.414
,