我们小学时就会加减乘除的笔算方法,那任意数开平方能笔算吗?今天我们就来说说任意数开平方怎么笔算。
首先我们的数字是十进制表示法,形如12的字符串ab表示数字10a b ,开平方的过程就是找到一个数字(用某字符串表示)使它的平方逼近已知数字。先将数字每两位分一节,之所以两位一节,是因为100(两位)是10(一位)的平方。例如1296,我们将其拆成两节,12看成一节,96看成一节。假设两位数字符ab的平方是1296,我们现在要确定出字符ab.笔算格式和除法相似,因为3的平方最接近12(就是1296的第一节),从而确定a=3 ,然后和除法一样下移数字,只是这里下移两位,移下来组成新数396,由于根的第一位已经确定,也就是10a b中的a已经确定,现在要确定b。因为(10a b)²=100a² 20ab b²=100a² (20a b)b,而100a²已经被从最高节中减掉了。因此对于余下的新数396,只需用(20a b)b来逼近396(即用66去除396),从而确定根的第二位b。具体过程是按下图操作,从而可以确定1296的平方根是36。

我们再举一例,求15129的平方根。先将数每两位分一节1,51,29;分成三节对应平方根是一个三位数(用字符abc表示),最高节1,对应根的最高位1(a=1),现在确定根的第二位和第三位(十位和个位),按照上例的方法确定根的第二位为2(b=2)。确定了b,接下来,再次相减,即把刚确定的(20a b)b减掉,从而再次获得新余数7,然后下移两位,移下来组成新数729。因为(100a 10b c)²=(100a 10b)² 2(100a 10b)c c²=(100a 10b)² 20(10a b)c c²=(100a 10b)² [20(10a b) c]c,所以再次将已经确定的根的前两位乘以20(即(10a b)×20 )加c ,用这个数除729,来确定平方根的第三位c(即用[20(10a b) c]c来逼近729),从而可以确定根的第三位c=3。具体过程如下(算出15129的平方根是123):

如果一个数的平方根有更多位,只需将上述方法重复,每一步的余数和被开方数的下一节(两位下移),组成新余数,再用已试出的根的前几位乘以20去除这个新余数,商几就将除数加几,再确定这一步的余数,循环计算直到余数为0或者无限循环计算下去(当然有开不尽的数)。
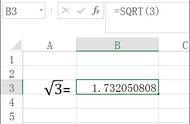
再比如计算5的平方根,(先将5的小数点后添0,变成更长的数),计算过程如下图:

以上就是任意数开平方的笔算方法,你学会了吗?
,