画出邻接矩阵存储示意图,邻接矩阵存储方法

有向图

存图的常见方法有两种：

1. 邻接矩阵

2. 邻接表

用一个n阶的方阵来存放图中各结点的关联信息。（如使用二维数组）

int g][];

若 R[ i ][ j ]

• 等于 1 ，表示结点 i 到结点 j 有一条邻接边（有向边）
• 等于 0 ，表示结点 i 到结点 j 没有邻接边

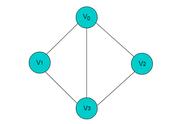
该图下标从1开始

如上图中，因为 1 到 2 和 2 到 1 有一条邻接边，所以有R[1][2] = R[2][1] = 1;

通过这样记录图可以得到上面的二维数组。

• 通过上面我们可以看出，无向图的邻接矩阵关于斜边对称。所以可以通过用上三角或下三角矩阵存无向图来节省空间。

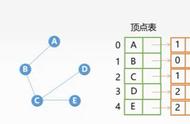
用链表来实现

• 首先把每个结点的邻接结点用一个链表表示出来，这时我们可以得到n个链表 （n为结点数）

• 然后用一个一维数组来顺序存储每个链表的头指针（即对应的结点）

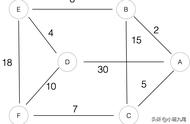
• 对于V1 结点，它的邻接结点有 V2、V4、V6，分别距离为6、1、50。

• 所以在V1的链表中，我们如下这样记录[2][6]--[4][1]--[6][50]（表示到达V2距离6，到达V4距离1，到达V6距离50）。

• 最后把所有链表放在一个一维数组中，得到如下的邻接表。