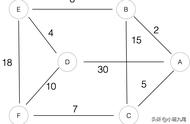
图的应用:社交网络,交通网络,活动网络……
图的分类:无向图(特殊有向图),有向图;有权图,无权图。特殊边—自环边
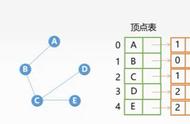
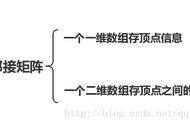
图的表示:邻接矩阵
完全图:音乐和电影相似推荐系统(每个电影和其他相连接)

稠密图:邻接矩阵,全排列空间最大。

class DenseGraph{ private: int n, m; //点和边 bool directed; //是否有向 vector<vector<bool>> g; //二维矩阵 public: DenseGraph( int n , bool directed ){ this->n = n; this->m = 0; //初始化,后续添加边 this->directed = directed; for( int i = 0 ; i < n ; i ) g.push_back( vector<bool>(n, false) ); //创建n*n矩阵 } ~DenseGraph(){ } int V(){ return n;} int E(){ return m;} void addEdge( int v , int w ){ assert( v >= 0 && v < n ); assert( w >= 0 && w < n ); if( hasEdge( v , w ) ) return; g[v][w] = true; if( !directed ) g[w][v] = true; m ; } bool hasEdge( int v , int w ){ assert( v >= 0 && v < n ); assert( w >= 0 && w < n ); return g[v][w]; } };
稀松图:邻接表,直接存储连接的节点,略节省空间

class SparseGraph{ private: int n, m; bool directed; vector<vector<int>> g; //存相邻节点 public: SparseGraph( int n , bool directed ){ this->n = n; this->m = 0; this->directed = directed; for( int i = 0 ; i < n ; i ) g.push_back( vector<int>() ); } ~SparseGraph(){ } int V(){ return n;} int E(){ return m;} void addEdge( int v, int w ){ assert( v >= 0 && v < n ); assert( w >= 0 && w < n ); if( hasEdge( v , w ) ) return; g[v].push_back(w); if( v != w && !directed ) //排除自环 g[w].push_back(v); m ; } bool hasEdge( int v , int w ){ //判定是否存在平行边 assert( v >= 0 && v < n ); assert( w >= 0 && w < n ); for( int i = 0 ; i < g[v].size() ; i ) if( g[v][i] == w ) //存在自环边 return true; return false; } }; ,