本文约2500字,建议阅读5分钟
本文对图神经网络基本概念以及典型的模型做简要的介绍。
图(Graph)是一种数据结构, 能够很自然地建模现实场景中一组实体之间的复杂关系。在真实世界中,很多数据往往以图的形式出现, 例如社交网络、电商购物、蛋白质相互作用关系等。因此,近些年来使用智能化方式来建模分析图结构的研究越来越受到关注, 其中基于深度学习的图建模方法的图神经网络(Graph Neural Network, GNN), 因其出色的性能已广泛应用于社会科学、自然科学等多个领域。
基本概念
1.1 图的基本概念
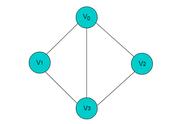
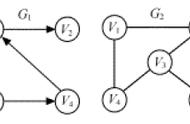
通常使用G=(V, E)来表示图,其中V表示节点的集合、E表示边的集合。对于两个相邻节点u, v, 使用e=(u,v)表示这两个节点之间的边。两个节点之间边既可能是有向,也可能无向。若有向,则称之有向图(Directed Graph), 反之,称之为无向图(Undirected Graph)。
1.2 图的表示
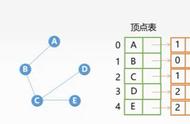
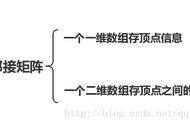
在图神经网络中,常见的表示方法有邻接矩阵、度矩阵、拉普拉斯矩阵等。
1)邻接矩阵(Adjacency Matrix)
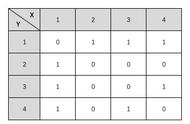
用于表示图中节点之间的关系,对于n个节点的简单图,有邻接矩阵

:

2)度矩阵(Degree Matrix)
节点的度(Degree)表示与该节点相连的边的个数,记作d(v)。对于n个节点的简单图G=(V, E),其度矩阵D为

,也是一个对角矩阵。
3)拉普拉斯矩阵 (Laplacian Matrix)
对于n个节点的简单图G=(V, E),其拉普拉斯矩阵定义为L=D-A,其中D、A为上面提到过的度矩阵和邻接矩阵. 将其归一化后有