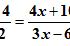分式方程增根与无解的区别
学习分式方程时,很多同学认为增根和无解是一回事,导致解题过程中出现了错误。那么,增根和无解到底有何区别呢?结合两个具体例子,我们加以分析和理解。
例1、当k为何值时,分式方程有增根?
【分析】分式方程两边乘以x(x﹣1)去分母转化为整式方程,由分式方程有增根得到x(x﹣1)=0,求出x=0或1,将x=0或1代入整式方程即可求出k的值.
【解答】解:方程两边同乘以x(x﹣1)得:6x=x 2k﹣5(x﹣1)…
又∵分式方程有增根,
∴x(x﹣1)=0,
解得:x=0或1
当x=1时,代入整式方程得:6×1=1 2k﹣5(1﹣1),
解得:k=2.5,
当x=0时,代入整式方程得:6×0=0 2k﹣5(0﹣1),
解得:k=﹣2.5,
则当k=2.5或﹣2.5时,分式方程有增根.
【点评】:这类题只需两步,第一步去掉分母化成整式方程,化成整式方程就不要再去变形整理了,保持“原状”不动,第二步找到增根,代入求解即可。
例2、已知关于x的分式方程﹣=1无解,则m的值为( )
A.0 B.0或﹣8 C.﹣8 D.0或﹣8或﹣4
【分析】分式方程无解的条件是:(1)、分式方程有增根(2)、去分母后所得整式方程无解。
【解答】解:方程去分母得:(x﹣2)2﹣mx=(x 2)(x﹣2),
根据增根的意义:当x=﹣2时分母为0,方程无解,即m=﹣8;
当x=2时分母为0,方程无解,即m=0
同时,我们进一步整理得:(4 m)x=8,
当m=﹣4时整式方程无解;
故选:D.
【点评】由此,我们不难看出,分式方程无解分两种情况:分式方程产生增根;整式方程本身无解。将分式方程化成整式方程后,一定进一步求解,找到整式方程无解的情况。
巩固练习:
1、(2018•潍坊)当m= 时,解分式方程=会出现增根.
2、关于x的分式方程﹣1=有增根,请求出增根及此时m的值
3、关于x的分式方程﹣=1 无解,则a的值是多少.
,