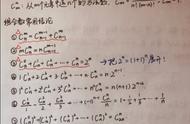一、教材引言的三个意图:
(1)通过生活中的实际例子,表明了现实中的计数问题普遍存在,学习一些计数知识是非常重要的;
(2)概述了研究计数问题的目的,即“如何能不通过一个一个地数而确定出这个数”,即要探究计数的技巧;
(3)明确了本章要学习的主要内容。

二、本章需要掌握的内容有:
3个重要原理(定理):分类加法计数原理、分步乘法计数原理、二项式定理;
6个重要概念:排列、排列数、组合、组合数、二项式系数、项的系数;
3个重要公式:排列数公式、组合数公式、二项展开式的通项;
5种重要关系:分类与分步、排列与组合、排列与排列数、组合与组合数、二项式系数与项的系数;
2个重要性质:组合数的性质、二项式系数的性质;
7种重要方法:列举法、树状图法、整体法、插空法、捆绑法、排除法、赋值法。

三、思想方法归纳
1,分类与整合的思想
在本章中,分类与整合的思想有着广泛的应用。应用分类与整合的思想解决问题,必须保证分类科学、标准统一、不重复、不遗漏,并力求简捷。
2,正难则反的思想方法
“正难则反”是一种重要的解题方法,即从问题的反面进行思考,通过排除,即可使诸多较复杂的计数问题简单化,当问题从正面考虑比较复杂,而反面比较简单时,可用这种方法解题。
3,化归与转化的思想
化归与转化的思想是指在解决问题的过程中,通过某种转化,把待解决或难解决的问题归结为一类已解决或易解决的问题。在解决排列、组合问题,特别是“至多”“至少”问题时,可以转化为从其反面考虑,用间接法求解。在与二项式定理有关的问题中,主要是多项式转化为二项式求解。
四、专题归纳总结
1,两个计数原理的应用
用两个计数原理解决问题的关键在于正确区分“分类与“分步”分类就是能“一步到位”——任何一类中任何一种方法都能完成整个事情;分步则只能“局部到位”——任何一步中任何一种方法只能完成事情的某一部分。分类要做到不重不漏,分步要做到“步骤完整”。
点评:计数问题的类型多样,在实际应用中,恰当分类,合理分步是解决计数问题的基本思路。以元素的性质或位置的不同分类,以事件发生的过程分步,正确使用两个计数原理及排列与组合计数。当问题既涉及排列又涉及组合时,一般采用“先组合后排列”的方法,即“先选后排”,可避免重复与遗漏。
2,排列组合问题
在解决一个实际问题的过程中,常常遇到排列、组合的综合性问题。解决此类问题时,只有认真审题,才能把握问题的实质,常用的方法有:
(1)合理分类,准确分步;
(2)特殊优先,一般在后;
(3)直接间接,灵活选择;
(4)元素相邻,捆绑为一;
(5)元素相间,插空解决;
(6)抽象问题,构造模型。
a,分行排列问题
将不同的元素排成若干行的排列问题,若没有特殊要求,则等价于所有元素的全排列。当元素有限制条件时,可优先安排特殊元素,再将其余元素全排列。
b,带有多个限制条件的计数问题
对于含有多个限制条件的计数问题,通常有两种解题途径:一是通过分析每个限制条件,分类或分步逐一满足各条件,利用直接法求解;二是先满足部分限制条件再排除不符合条件的计数,即利用部分排除法求解。
点评:排队问题中的限制条件主要是某人在或不在某位置,可采用位置分析法或元素分析法进行排列。对相邻、相间、定序、分排等常见问题的解法应记住。相邻元素“捆绑”,不相邻元素“插空”,特殊位置、特殊元素优先处理。
c,错位排列问题
所谓错位排列问题是元素编号与位置编号都不一致的一种排列问题,当元素个数较少时可采用枚举法计数。
d,圆排列问题
所谓圆排列,即n个不同的元素围成一个圆圈时的排列,它与按顺序排成一列的排列是不同的,因为圆排列中按1-2-3的排列与按2-3-1,3-1-2的排列是一样的图形。(如图6-4-3)

所以其排列方法数比我们熟悉的排列方法数要少。一般地,n个元素的圆排列,其排法有(n-1)!种。下面使用递归的方法,推导这个公式。
从最简单的推起:当圆排列只有一个人时,显然只有一种排法,即(1-1)!,两个人时也只有一种排法,即(2-1)!。

为了清晰表示这种情况,用简单的图形(图6-4-4)表示,可以基于下面的思路:三个人圆排列时,可以看成是在前面两个人圆排列的基础上再加一个人,两个人圆排列时有(2-1)!种排法,同时两个人之间形成两个空隙,第三个人只需在两个空隙中任选一个空隙坐下即可,故三个人的圆排列有2×(2-1)!=(3-1)!种。同理,四个人圆排列时,可以看成是在三个人圆排列的基础上再加一个人,三个人的圆排列有(3-1)!种,同时三个人之间会形成三个空隙,我第四个人可以从三个空隙中任选一个坐下,故四个人的圆排列有3×(3-1)!=(4-1)!种,依次类推,n个人圆排列时,可以看成是在(n-1)个人圆排列的基础上再加一个人,(n-1)个人的圆排列有(n-2)!种,同时(n-1)个人之间会形成(n-1)个空隙,第n个人可以从(n-1)个空隙中任选一个坐下,故n个人的圆排列有(n-1)×(n-2)!=(n-1)!种。
3,二项式定理及其应用
求二项展开式的特定项通常是先根据条件求r,再求Tr 1,有时还需先求n,再求r,才能求出Tr 1。有些多项式问题可以通过变形变成二项式问题加以解决,有时也可以通过组合解决。
4,二项式系数的性质
对于二项式系数的问题,首先要熟记二项式系数的性质,其次要掌握赋值法,赋值法是解决二项式系数问题的重要方法。
,