在我们的初中数学教学课程中,我们会学习到公因式这个重要的知识点,它的我们分解因式的关键,那么什么是公因式呐?是只有多项式才有的,是指这个多项式中各项都具有的公共因式。它可以是一个单项式,也可以是一个多项式,还可以是一个单项式与一个多项式的积。那么我们该如何求解公因式呐,下面我就为大家介绍一下:

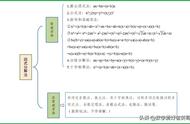
首先,我们了解一下公因式的求法:
系数:各项系数的最大公约数;
字母:各项都含有的字母;
指数:相同字母的最低次幂。
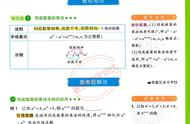
提公因式法:一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法叫做提公因式法。
确定公因式的一般步骤:
(1)如果多项式是第一项系数是负数时,应把公因式的符号“-"提取。
(2)当各项系数都是整数时,取多项式各项系数的最大公约数为公因数的系数。
(3)把多项式各项都含有的相同字母(或因式)的最低次幂的积作为公因式的因式。
上述步骤不是绝对的,当第一项是正数时步骤(1)可省略。
注意:如果多项式的第一项是负的,一般要提出负号,使括号内第一项系数是正的。提出“-”号时,多项式的各项都要变号。
例:3x 6 x y xy 1
=3(x 2) (x xy) (y 1)
=3(x 2) x(1 y) (y 1)
=3(x 2) (x 1)(y 1)
可见提公因式法也是需要一定的技巧。
再看一道例题:
(x-y)2 y-x
=(y-x)2 (y-x) (技巧就在这一步)
=(y-x 1)(y-x)
注意:如果多项式的第一项是负的,一般要提出负号,使括号内第一项系数是正的。

口诀:
找准公因式,一次要提净;
全家都搬走,留1把家守;
提负要变号,变形看奇偶。
接着,为大家介绍游戏提取公因式法的解题步骤:
提取公因式法是因式分解的一种基本方法。如果多项式的各项有公因式,可以把这个公因式提取出来作为多项式的一个因式,提取公因式后的式子放在括号里,作为另一个因式。提取公因式是乘法分配律的逆运算,其最简形式为:ma mb mc=m(a b c)。
利用提公因式法分解因式时,一般分两步进行:
(1)提公因式:
把各项中相同字母或因式的最低次幂的积作为公因式提出来;
当系数为整数时,还要把它们的最大公约数也提出来,作为公因式的系数;
当多项式首项符号为负时,还要提出负号。
(2)用公因式分别去除多项式的每一项,把所得的商的代数和作为另一个因式,与公因式写成积的形式。
由于题目形式千变万化,解题时也不能生搬硬套。
例如,有的需要先对题目适当整理变形;
有的分解因式后多项式因式中有同类项的还要进行合并化简;
还有的提取公因式后能用其他方法继续分解。

以上就是公因式的一些基本求解方式方法,希望大家能够掌握,掌握这些内容对大家解决因式分解会有很大的帮助,只有我们不断的积累,我们才能学好数学,让我们一起努力吧。
,