本文讲述了数据分析师应当了解的五个统计基本概念:统计特征、概率分布、降维、过采样/欠采样、贝叶斯统计方法。
从高的角度来看,统计学是一种利用数学理论来进行数据分析的技术。象柱状图这种基本的可视化形式,会给你更加全面的信息。但是,通过统计学我们可以以更富有信息驱动力和针对性的方式对数据进行操作。所涉及的数学理论帮助我们形成数据的具体结论,而不仅仅是猜测。
利用统计学,我们可以更深入、更细致地观察数据是如何进行精确组织的,并且基于这种组织结构,如何能够以最佳的形式来应用其它相关的技术以获取更多的信息。今天,我们来看看数据分析师需要掌握的5个基本的统计学概念,以及如何有效地进行应用。
特征统计
特征统计可能是数据科学中最常用的统计学概念。它是你在研究数据集时经常使用的统计技术,包括偏差、方差、平均值、中位数、百分数等等。理解特征统计并且在代码中实现都是非常容易的。请看下图:

上图中,中间的直线表示数据的中位数。中位数用在平均值上,因为它对异常值更具有鲁棒性。第一个四分位数本质上是第二十五百分位数,即数据中的25%要低于该值。第三个四分位数是第七十五百分位数,即数据中的75%要低于该值。而最大值和最小值表示该数据范围的上下两端。
箱形图很好地说明了基本统计特征的作用:
- 当箱形图很短时,就意味着很多数据点是相似的,因为很多值是在一个很小的范围内分布;
- 当箱形图较高时,就意味着大部分的数据点之间的差异很大,因为这些值分布的很广;
- 如果中位数接近了底部,那么大部分的数据具有较低的值。如果中位数比较接近顶部,那么大多数的数据具有更高的值。基本上,如果中位线不在框的中间,那么就表明了是偏斜数据;
- 如果框上下两边的线很长表示数据具有很高的标准偏差和方差,意味着这些值被分散了,并且变化非常大。如果在框的一边有长线,另一边的不长,那么数据可能只在一个方向上变化很大
概率分布
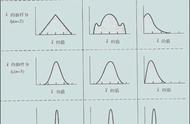
我们可以将概率定义为一些事件将要发生的可能性大小,以百分数来表示。在数据科学领域中,这通常被量化到0到1的区间范围内,其中0表示事件确定不会发生,而1表示事件确定会发生。那么,概率分布就是表示所有可能值出现的几率的函数。请看下图: