什么情况下用导函数,什么情况下导函数不存在

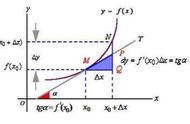
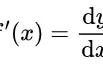自从导数相关知识内容进入高中数学课本以来，因其能使很多复杂问题变得简便化，大大提高解题效率，自然成为老师和学生重点学习方法，更受到高考数学命题老师的青睐。

我们对近几年的高考数学试卷进行分析和研究，与导数知识有关的题型已成为高考数学的热点，其运用非常广泛。常见的考点有函数的单调性、函数的最值、切线方程及不等式等问题，能够很好的考查学生实践能力，体现了高考选拔人才的功能。

像函数的单调性主要讲以下这些知识内容：

在(a，b)内可导函数f(x)，f′(x)在(a，b)任意子区间内都不恒等于0.

f′(x)≥0⇔f(x)在(a，b)上为增函数．

f′(x)≤0⇔f(x)在(a，b)上为减函数．

值得注意，由于近年来高考数学的导数与函数问题都与字母系数问题联系在一起，直接增加了题目的难度，让很多考生感到无从下手。

近几年的高考数学，无论是全国卷还是各省市卷，都在逐年加大对导数问题的考查力度，不仅题型在变化，而且问题的难度、深度与广度也在不断加大。

导数相关的高考数学题，讲解分析1：

已知函数f(x)＝(2－a)ln x＋1/x＋2ax(a∈R)．

(1)当a＝0时，求f(x)的极值；

(2)求f(x)的单调区间．

解：(1)∵当a＝0时，f(x)＝2ln x＋1/x，

f′(x)＝2/x－1/x²＝（2x－1）x²(x>0)，

∴f(x)在（0,1/2）上是减函数，在（1/2， ∞）上是增函数．

∴f(x)的极小值为f（1/2）＝2－2ln 2，无极大值．

(2)f′(x)＝（2－a）/x－1/x²＋2a＝（2x－1）（ax 1）/x²(x>0)．

①当a≥0时，f(x)在（0,1/2）上是减函数，在（1/2， ∞）上是增函数；

②当－2<a<0时，f(x)在（0,1/2）和（－1/a， ∞）上是减函数，在（1/2，－1/a）上是增函数；

③当a＝－2时，f(x)在(0，＋∞)上是减函数；

④当a<－2时，f(x)在（1/2， ∞）和（0，－1/a）上是减函数，在（－1/a，1/2）上是增函数．

如何求函数的极值？

1、函数的极小值：

函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其它点的函数值都小，f′(a)＝0，而且在点x＝a附近的左侧f′(x)＜0，右侧f′(x)＞0，则点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．

2、函数的极大值：

函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近的其他点的函数值都大，f′(b)＝0，而且在点x＝b附近的左侧f′(x)＞0，右侧f′(x)＜0，则点b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．

极小值点，极大值点统称为极值点，极大值和极小值统称为极值．

导数相关的高考数学题，讲解分析2：

设函数f(x)＝ln x－p(x－1)，p∈R.

(1)当p＝1时，求函数f(x)的单调区间；

(2)设函数g(x)＝xf(x)＋p(2x²－x－1)，对任意x≥1都有g(x)≤0成立，求p的取值范围．

解：(1)当p＝1时，f(x)＝ln x－x＋1，其定义域为(0，＋∞)．

所以f′(x)＝1/x－1.

由f′(x)＝1/x－1>0得0<x<1，由f′(x)<0得x>1.

所以函数f(x)的单调递增区间为(0,1)，单调递减区间为(1，＋∞)．

(2) 由函数g(x)＝xf(x)＋p(2x²－x－1)＝xln x＋p(x²－1)(x>0)，

得g′(x)＝ln x＋1＋2px.

由(1)知，当p＝1时，f(x)≤f(1)＝0，

即不等式ln x≤x－1成立．

①当p≤－1/2时，g′(x)＝ln x＋1＋2px≤(x－1)＋1＋2px＝(1＋2p)x≤0，

即函数g(x)在[1，＋∞)上单调递减，从而g(x)≤g(1)＝0，满足题意；

②当－1/2<p<0时，若x∈（1，－1/2p），则ln x>0，1＋2px>0，

从而g′(x)＝ln x＋1＋2px>0，即函数g(x)在（1，－1/2p）上单调递增，从而存在x₀∈（1，－1/2p）使得g(x₀)>g(1)＝0，不满足题意；

③当p≥0时，由x≥1知g(x)＝xln x＋p(x²－1)≥0恒成立，此时不满足题意．

综上所述，实数p的取值范围为（－∞，－1/2）

什么是函数的最值？

1、在闭区间[a，b]上连续的函数f(x)在[a，b]上必有最大值与最小值．

2、若函数f(x)在[a，b]上单调递增，则f(a)为函数的最小值，f(b)为函数的最大值；若函数f(x)在[a，b]上单调递减，则f(a)为函数的最大值，f(b)为函数的最小值．

​导数相关的高考数学题，讲解分析3：

设f(x)＝2x³＋ax²＋bx＋1的导数为f′(x)，若函数y＝f′(x)的图象关于直线x＝－1/2对称，且f′(1)＝0.

(1)求实数a，b的值；

(2)求函数f(x)的极值．

解：(1)因为f(x)＝2x³＋ax²＋bx＋1，

故f′(x)＝6x²＋2ax＋b，

从而f′(x)＝6（x a/6）²＋b－a²/6，

即y＝f′(x)关于直线x＝－a/6对称．

从而由题设条件知－a/6＝－1/2，即a＝3.

又由于f′(1)＝0，即6＋2a＋b＝0，

得b＝－12.

(2)由(1)知f(x)＝2x³＋3x²－12x＋1，

所以f′(x)＝6x²＋6x－12＝6(x－1)(x＋2)，

令f′(x)＝0，

即6(x－1)(x＋2)＝0，

解得x＝－2或x＝1，

当x∈(－∞，－2)时，f′(x)>0，

即f(x)在(－∞，－2)上单调递增；

当x∈(－2,1)时，f′(x)<0，

即f(x)在(－2,1)上单调递减；

当x∈(1，＋∞)时，f′(x)>0，

即f(x)在(1，＋∞)上单调递增．

从而函数f(x)在x＝－2处取得极大值f(－2)＝21，

在x＝1处取得极小值f(1)＝－6.

掌握好导数相关知识，可以帮助我们在解一些函数问题、不等式问题、解析几何问题等问的时候，提供了新的视角、新 的方法，拓宽了高考的命题空间。