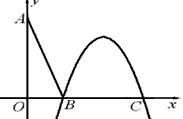
这是一个常规的零点个数转化为图像交点个数的问题,只是题目中出现的正切该如何处理需要好好地构思一下,动直线与x轴的交点就是x2,当直线与曲线恰好相切时共三个交点,选取x3作为切点的横坐标,利用共点和同斜率即可得到一个正弦和一个余弦,相除即可得到正切,所求正切值可转化为与x3有关的式子,再确定出x3的范围即可。


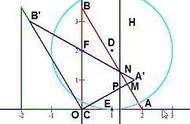
注意解析几何小题在考试中是不配图的,题目有一个常见的结论,即双曲线的交点到渐近线的距离为b,在本题中可写出过F点且与渐近线垂直的直线,两条直线联立即可求出M点坐标,利用M点是NF的中点,即可表示出N点的坐标,将N点坐标带入双曲线方程中化简即可得到离心率的值。(但实际解起来很不容易,因此这种是最容易想到的也是最费时间的方法)

根据结论可知ME=b,NF=2b,连接N点与左焦点F',则OM是中位线,即NF'=2a,在焦点三角形中利用定义可求得NF=4a,因此NF有两种不同的表示形式,即2b=4a,求出离心率的值即可。