在初中数学的课本中,我们会接触到三角形,四边形,等多边形图形,会出现两个角互为余角,互为补角的情况,但是他们有什么特点呐,下面我为大家做一下介绍:

余角:
如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
∠A ∠C=90°,∠A= 90°-∠C ,∠C的余角=90°-∠C 即:∠A的余角=90°-∠A
补角:
如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角
∠A ∠C=180°,∠A= 180°-∠C ,∠C的补角=180°-∠C 即:∠A的补角=180°-∠A

补角的性质:
同角的补角相等。比如:∠A ∠B=180°,∠A ∠C=180°,则:∠C=∠B。
等角的补角相等。比如:∠A ∠B=180°,∠D ∠C=180°,∠A=∠D则:∠C=∠B。
余角的性质:
同角的余角相等。比如:∠A ∠B=90°,∠A ∠C=90°,则:∠C=∠B。
等角的余角相等。比如:∠A ∠B=90°,∠D ∠C=90°,∠A=∠D则:∠C=∠B。
注意:
①钝角没有余角;
②互为余角、补角是两个角之间的关系。如∠A ∠B ∠C=90°,不能说∠A、∠B、∠C互余;同样:如∠A ∠B ∠C=180°,不能说∠A、∠B、∠C互为补角;
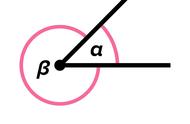
③互为余角、补角只与角的度数相关,与角的位置无关。只要它们的度数之和等于90°或180°,就一定互为余角或补角。

余角与补角概念认识提示:
(1)定义中的“互为”一词如何理解?
如果∠1与∠2互余,那么∠1的余角是∠2 ,同样∠2的余角是∠1 ;如果∠1与∠2互补,那么∠1的补角是∠2 , 同样∠2的补角是∠1。
(2)互余、互补的两角是否一定有公共顶点或公共边?
两角互余或互补,只与角的度数有关,与位置无关。
(3)∠1 ∠2 ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
不能,互余或互补是两个角之间的数量关系。
以上就是关于余角和补角的介绍,希望这些内容对大家在以后数学试题的练习中,会起到一定的帮助,祝大家学业有成。
,