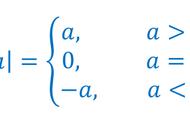与三角形中塞瓦线相关的线段倒数和5例
题目1:如下图,△ABC为等腰三角形,AB=AC,DE为△ABC的中位线,点P为DE上的动点,BP的延长线交AC于点N,CP的延长线交AB于点M。证明:1/BM 1/CN为定值。

解题思路:因AB=AC,DE为△ABC的中位线,则
DE=1/2 BC,BD=CE=1/2AB=1/2AC。
易证△MPD∽△MCB,△NPE∽△NBC,则
DM/BM=DP/BC,
EN/CN=EP/BC,
上述2式相加得:
DM/BM EN/CN=(DP EP)/BC=DE/BC=1/2。
将等式左边变形为:
(BM-BD)/BM (CN-CE)/CN=1/2,
BD/BM CE/CN=3/2。将BD、CE用1/2AB代替,则
1/BM 1/CN=3/AB,因AB为定值,
故1/BM 1/CN为定值。
题目2:如下图,O为锐角△ABC的外心,若AO、BO、CO分别交对边于D、E、F,设R为圆O的半径,求证1/AD 1/BE 1/CF = 2/R。

解题思路:详见。
题目3:如下图,在凸四边形ABCD中,边BA、CD的延长线相交于点P,两条对角线相交于点M,直线PM分别交AD、BC于点T、S。求证:2/PM=1/PT 1/PS。

解题思路:欲证倒数等量关系2/PM=1/PT 1/PS的三条线段位于线段PS上,P、T、M、S四点组成的线段有PS/MS=PT/MT的等量关系,先证明如下。
- PS/MS的代数表达式
根据燕尾定理公式,结合比例性质(等比性质):
PS/MS=S△PBS/ S△MBS= S△PCS/ S△MCS
=( S△PBS S△PCS)/( S△MBS S△MCS)
= S△PBC/ S△BMC,即
PS/MS = S△PBC/ S△BMC。
同理BD/DM= S△PBC / S△PMC。
AP/AB= S△PMC / S△BMC(详见)。
(2)PT/MT的代数表达式
图1中可见,△PBM被线段AD所截,根据梅涅劳斯定理得:
AP/AB·BD/DM·MT /PT = 1,即
PT/MT= AP/AB·BD/DM
= S△PMC / S△BMC·S△PBC / S△PMC
= S△PBC / S△BMC,即
PT/MT = S△PBC / S△BMC,则
PS/MS=PT/MT成立。
再将上式进行变形为:
MS/PS=MT/PT,
(PS-MP) /PS=(MP-PT) /PT,
1- MP /PS=MP /PT -1,
MP /PS MP /PT=2,
2/MP=1/PT 1/PS成立。
题目4:如下图,在凸四边形ABCD中,边BA、CD的延长线相交于点P,两条对角线相交于点M,直线PM分别交AD、BC于点T、S,连接AS、DS分别交BD、AC于点E、F。
求证:1/MT - 1/MS = 1/EM - 1/DM = 1/FM - 1/AM。

解题思路:参考题目3中的结论,详见三角形三条塞瓦线交于一点所构成图形的相关线段比例关系(三)。
题目5:如图,在△ABC中,AD平分∠BAC交BC于D,O为AD上一点,连接BO、CO并延长分别交AC于E、AB于F。证明:1/AF 1/AC=1/AE 1/AB。

解题思路:采用逆推法,用等量代换将上述等量关系依次变形运算如下。
1/AF 1/AC=1/AE 1/AB,
1/AF-1/AB=1/AE-1/AC(等式左侧线段AB含AF,等式右侧线段AC含AE),
(AB-AF)/AB·AF = (AC-AE)/AC·AE,
BF/AB·AF = CE/AC·AE,
BF/ AF = CE/ AE·AB/AC。
因AD为∠BAC的平分线,根据角平分线定理,则AB/AC=BD/CD,代入上式,则
BF/ AF = CE/ AE·BD/CD,
CE/ AE·AF/BF·BD/CD=1。
该等式即为塞瓦定理的表达式,如果再将其逆推,即可证明本题的结论成立,再次不再赘述。
,