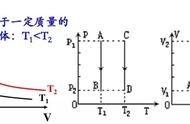
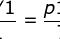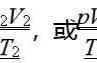理想气体状态方程是描述气体状态的基本方程,它可以用来计算气体的压强、体积、温度和物质的摩尔数之间的关系。其推导过程如下:
1.假设气体分子是一个个质量很小的粒子,它们在容器内自由运动,并与容器壁和其他气体分子发生碰撞。
2.根据动量定理,气体分子的撞击会改变它们的动量,但总动量守恒。因此,气体分子的平均动量与温度有关。
3.根据玻尔兹曼分布定律,气体分子的速度分布服从麦克斯韦-玻尔兹曼分布,即速度的概率密度函数为:
f(v) = 4π (m/2πkT)^(3/2) v^2 exp(-mv^2/2kT)
其中,m为气体分子的质量,k为玻尔兹曼常数,T为气体的绝对温度,v为气体分子的速度。
4.假设气体分子在x、y、z三个方向上的速度分量是独立的,即速度分量之间没有相关性。则气体分子的动能可以表示为:
K = (1/2) m (vx^2 vy^2 vz^2)
根据平均定理,气体的压强等于气体分子对容器壁的平均撞击力,即:
P = (1/3) nm<vx^2>
其中,n为气体的摩尔数,<>表示取平均值。
将步骤4中的动能代入步骤5中,得到:
P = (1/3) nm<v^2>
根据理想气体的定义,气体分子之间不存在相互作用力,因此它们之间的平均距离很大,可以忽略它们之间的体积。因此,气体的体积可以表示为:
V = n<1/m>
将步骤6和步骤7中的式子代入理想气体状态方程PV=nRT中,得到:
P V = (1/3) n m <v^2> = (2/3) K
其中,K为气体分子的平均动能。
将步骤8中的式子进一步化简,得到:
PV = NkT
其中,N为气体分子的数目,k为玻尔兹曼常数,T为气体的绝对温度。这就是理想气体状态方程的最终形式。
,