一次函数是初二同学开始接触的第一个函数,刚开始的时候很多同学对这部分的知识,或多或少对有些知识会有一些遗忘或者对这部分的内容掌握并不是很好,今天给大家分享一下关于初二数学下一次函数与代数综合的培优,适合基础中等或者想要拔高的同学,适合人教新版的学生,由于篇幅有限,今天先分享的是第一个模块:一次函数的图像变换
我们先来梳理一下这部分内容的知识点,请各位同学务必对以下的知识点理解透彻并达到熟悉的程度。
模块一:一次函数图像的变换及特殊位置关系:
1.平移:上加下减,左加右减;
2.对称:关于哪轴对称那轴对应坐标不变,另外一个变为原来的相反数;
3.中心对称:x和y值都变.
4.三大变换通解方法:找两个点(如与坐标轴的两个交点),进行相应变化后,再确定解析式.
5.特殊位置关系:
(1)若两直线平行:k(斜率)相等(b值不等).
(2)若两直线垂直:两直线k(斜率)互为负倒数,即k1*k2=-1.
对于知识是否熟悉掌握和灵活运用,最后都要落实到做题上面·,以下是关于模块一的部分练习:
【例1】
(1)把函数yy=-2x 4的图象向上平移2个单位,所得函数图象的解析式为_________;
(2)把函数y=3x 4的图象向右平移2个单位,所得函数图象的解析式为_________;
(3)把函数-3x-1的图象向左平移3个单位,再向下平移2个单位,所得函数图象的解析式为__________;
(4)若将直线l的图象向右平移3个单位,再向上平移2个单位后,得到直线y=-2x 1,则原直线解析式为__________.
【答案】(1)y=-2x 6;(2)y=3x-2;(3)y=-3x-12;(4)y=-2x-7.
【注意】:这道题主要考查一次函数的平移规律:上加下减,左加右减.规律可以记不住,但是同学们一定要本质,通过寻找特殊点(一般是与坐标轴交点)变换后的点,运用两点式或点斜式来确定直线的解析式。
【例2】
(1)若直线y=kx(k不为0)经过点(1,3),则该直线关于轴对称的直线解析式为______.
(2)函数y=-x 2的图象关于y轴对称,得到的函数图象的解析式为____________.
(3)函数y=2x-3的图象先关于y轴对称,再关于x轴对称,得到函数的解析式为____
________.
【答案】(1)将点关于x轴对称,得到(1,-3),∴解析式为y=-3x.
(2)y=x 2.
(3)y=2x 3.
【注意】:这道题主要考查一次函数的对称规律:关于哪轴对称哪个不变.
【例3】
(1)直线yy=2x-3关于(0,0)对称的直线的解析式为:__________.
(2)直线y=k1x b1(k1不为0)与直线y2=k2x b2(k2不为0)平行,则k1( )k2.
(3)直线l平行于直线y=-2x,且过点(4,5),则l的解析式为__________.
(4)直线y=k1x b1(k1不为0)与直线y2=k2x b2(k2不为0)垂直,则k1*k2=( ).
(5)直线l垂直于直线y=3x 2,且过点(1,4),则l的解析式为__________.
(6)点A(1,2)关于直线y=-x 5的对称点A'的坐标是__________.
【答案】(1)y=2x 3; (2)=;
(3)y=-2x 13; (4)-1;
(5)y=-1/3x 13/3; (6)(3, 4).
【注意】:要求同学们记住一次函数中特殊情况的基本结论.平移、轴对称、及中心对称变换的通用解法:找两个点(如与坐标轴的两个交点),也相应变化后,确定解析式.最后,学会点关于直线对称的求解方法(点斜式或两点式,垂直 中点).
今天就先给大家分享到这里,相对来说,难度还不大,希望大家要把今天分享的内容都吃透,有所收获。
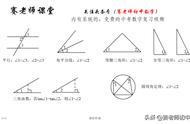
可能部分同学对一次函数的一些基本知识会有所遗忘,所以下列各大家做了一个简单的图,作为回顾,需要的同学可以收藏一下,加油。

图1
,