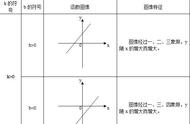
多参数不要怕,步步为“赢”

在数学压轴题中,存在这么一类题型,函数背景,含有若干参数,与三角形、四边形结合,简单可称为“含参函数几何形”,既考察函数综合,也包含数形结合思想,其中参数的个数不低于1个,而学生在考试期间,最怵的也是这类题型,众多参数,再加上对函数图象的理解不够深刻,极易出现看不懂题,或者理解错误的情况。
然而这些题目,只是看上去很吓人,只要认真读题,按常规思路一步步坚定地走下去,完成解答并不如他们口中的“太难了”。
题目
已知:A(-2,2),B(-4,1),C(-2,0),D(0,1).
(1)直接写出四边形ABCD的面积和直线AB的解析式;
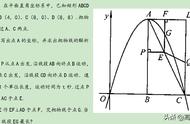
(2)如图,若点M(m 4,n-2)与点N关于原点对称,过M、N两点的抛物线y=ax² bx c与y轴相交于点C.
①当射线BC过点E时,点P(m 3,n 1)是边AB上一动点(可以与点A,B重合),求a的取值范围及n-m的最大值;
②求证:过点E且与抛物线y=ax² bx c有且只有一个公共点的直线或与x轴垂直,或与直线MN平行.

解析:
(1)各种补形求面积法,横竖都可,结果为4,直线AB解析式为y=1/2x 3;
(2)我们先逐句解读题目条件,再看两个小问题的分支条件,由于M、N两点关于原点对称,因此可写出点N坐标为(-m-4,-n 2),且这两个点都在抛物线上,所以我们将它们分别代入解析式中,得两个方程如下:
a(m 4)² b(m 4) c=n-2;
a(-m-4)²-b(m 4) c=-n 2;
以上点N坐标和两个方程备用,再来看分支条件:
①射线BC经过点E,我们可先求出直线BC的解析式,为y=-1/2x-1,它与y轴交点为(0,-1),因此E(0,-1),于是抛物线解析式中的参数c=-1,原来的两个方程消元后如下;
a(m 4)² b(m 4)-1=n-2;
a(-m-4)²-b(m 4)-1=-n 2;
整理得a=1/(m 4)²;
点P(m 3,n 1)是边AB上一动点,不妨将点P坐标代入直线AB解析式中,得n=1/2m 7/2,说明参数n可以消掉,用表示;
动点在边AB上,存在范围,分别观察点A和点B横坐标,得-7≤m≤-5,而我们已经用含m的代数式表示出了a,并且在这个范围内,a的值逐渐增大。
强调:a的值逐渐增大,这个结论是利用二次函数图象的性质,我们知道(m 4)²若看作二次函数,在m<-4时随m的增大而减少,然而它在分母中,整个分式的值反而逐渐增大。
对于n-m,我们可以将它化为-1/2m 7/2,当m=-7时,n-m取最大值为7;
②没有射线BC经过点E的条件,也意味着参数c第一时间无法消掉,我们仍然利用加减法消元,得到b=(n-2)/(m 4),c=-a(m 4)²
过点E的直线,并且这条直线和抛物线只有唯一公共点,我们可设这条直线为y=kx-a(m 4)²,将之与抛物线联立,得:
kx-a(m 4)²=ax² bx-a(m 4)²
整理得ax² (b-k)x=0
△=(b-k)²=0,得k=b=(n-2)/(m 4)
于是这条直线为y=(n-2)/(m 4)x-a(m 4)²
那么直线MN解析式我们也可用含m、n的代数式表示为
y=(n-2)/(m 4)x
通过比较它们的一次项系数,发现相等,于是这是一组平行线;
而众所周知,抛物线与y轴只有唯一公共点,所以结论成立。
解题反思:
这道题最大的障碍在于参数众多,但解完之后我们却发现,多数参数并不需要求出数值,第二问中得到的两个方程,出现多个相同项和相反项,加减消元法效果神奇,如果把对参数的畏惧消除了,此题并不算难。
关于函数背景下的平行关系,我们想到最多的是两个一次函数图象,而在教材上,出现的地方在八年级下册91页例2,只是它的背景是平移,并且用到“倾斜程度”来描述,如果以此来拓展,的确可以得到两个一次函数图象平行,则k值相同。


教材中第二次出现关于直线“倾斜程度”在九年级三角函数,站在整个初中学段来看,倾斜程度与三角函数之间肯定存在关联,我们知道在高中,这个k值也称斜率。
关于抛物线与y轴的交点问题,我们知道,初中阶段的抛物线,与y轴有且只有一个公共点,稍拓展一点,任何与y轴平行的直线,与抛物线都有且只有一个公共点。
如果在学习二次函数图象与性质的时候,没有足够的理解,这道题显然很难,因此我们平时的课堂教学中,需要引导学生细致观察图象,得到必要的信息,这些信息并不是靠口诀记下来,而是通过操作进行认知,须知功夫要下在平时,才能步步为“赢”。
*爱数学做数学
,