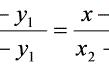平行对学生来说不陌生,平行现象在生活中也很常见。平行是对众多平行现象的本质分析,摆在我们面前的问题,平行到底是什么?《几何原本》中的第五公设说的也是平行:“同一平面内一条直线和另外两条直线相交,若在直线同侧的两个内角之和小于180°,则这两条直线无限延长后在这一侧一定相交。”教材中的定义是这样:“同一平面内不相交的两条直线互相平行”。两种定义都不是很好理解,当然我指的是小学生。既然小学生很难理解,我们一定要这样定义吗?我想,我们是小学数学工作者,不是数学家,大可不必从数学家的角度去定义数学概念。我们的目的是让学生享受数学教育,而不是害怕数学,当然这与数学教育的“以知怡情”不矛盾。那我们该怎样定义平行呢?解决这个问题之前我们先研究一下怎样才不平行,按教材中的说法,相交就是不平行,且不说“相交”本身就是一个概念,以概念解释概念,难度还是很大的。这里我们看这句话“不相交就是平行”,这只是用一种现象概括另一种现象,并不涉及平行的本质。
下面的例子对大家理解平行会有帮助(图—1):

(图—1)
红线和黑线不平行,为什么不平行,把红线向上平移,与黑线碰在一起形成一个角。什么是角?由一点向不同方向引出两条射线组成的图形叫做角,这也就是说两条直线角度不同就会碰在一起,即相交。平行线在儿童眼里无非两种情况,一是水平、二是竖直。这两种情况以外的平行线儿童都会以这两种情况为参照,这时在儿童那里便出现了表示方向的“角度”。在儿童眼里黑线和红线不平行是因为角度不同,这里的角度就是指黑线与红线相对于水平方向的角度,那也就是方向。这里老师可以点明“你们是不是想说它们的方向不同,所以才不平行”。在数学上,同一平面内不平行又叫相交,相交的情况有很多,其中有一种很特殊,那就是相交成直角着这种情况。在实际生活中这样的例子也有很多,如双杠的水平杠与立柱、椅子腿与横木等。你能把这样的两条线画下来吗?
……
对于“平行与垂直”的教学老师们顾及最多的还是教材中的定义,教学时我们要以学生的视角认识平行与垂直。对于教材中关于平行的概念可以不予考虑,只是在学生得出平行定义后与教材概念进行对比即可。教材中的平行定义是这样的“同一平面内不相交的两条线叫平行线”。这只是分类后的重新命名,平行的真正内涵并没有讲出来。在课上,老师问学生“我们能找到平行,也会画平行线,你知道怎样才会平行吗?”学生说“角度相同就平行”。上面已经讲过儿童所谓的“角度”就是方向,这才是平行的本质,至少儿童是这么认为的。这就又涉及另一个话题,我们到底以什么视角来设计教学。我们不是从数学家的角度为数学定义,而是为儿童真正享受数学的角度设计教学。
什么是数学?美国数学家柯朗·罗宾写了一本书《什么是数学》,他认为“最好的数学就应该像文学作品——故事来源于眼前活生生的生活,致使你把精力与感情投入其中”。逻辑与直观是数学的重要特点,这就告诉我们,数学对象是什么并不重要,重要的是我们做了什么,这样数学就艰难的徘徊在现实与理论之间。对于小学阶段的数学,我们更应该靠近现实,但靠近现实不是目的,数学的目的是学会数学的思维,即抽象。小学数学靠动作抽象,这也就是皮亚杰说的“反观动作后的反身抽象”。对于平行的认识,教材让学生“任意画两条直线,会有哪几种情况?”从教材的第一句话就可以感觉到,教材是从“分类”的角度,逐步确定概念的外延,然后再对外延进行重命名。这样认识平行,表面是发挥学生的想象力,实则亦步亦趋跟着老师走。平行的本原是什么,换句话说平行的本质是什么,我一直认为平行与垂直是对直线方向性的一次再认识。第一次认识直线方向是在二年级学习“角”,角的定义是这样:从一点向不同方向引出两条射线,组成的图形叫做角。射线有方向,射线的同宗直线、线段同样有方向。第二次认识直线方向在四年级“平行与垂直”,对直线方向性进行一次梳理,并对其中两种特殊情况——平行与垂直,进行深入的认识。在现实中,学生对“平行”认识到什么程度呢?在课堂上,学生都能找到生活中的平行,尤其学生在用两根小棒摆平行时,几乎都在利用已有的平行关系。例如,有的学生将两根小棒分别摆在两条斑马线上,有的学生将两根小棒摆在长方形的两条长边上……这说明学生对平行有较深刻的认识,接下来再逐步深入认识平行。
在实际教学中,用小棒摆平行时有的同学只是“看着平行”,并不借助任何平行关系,或是平行工具去再现平行。这是不对的,看着平行在数学上行不通,数学需要证明。数学证明有两个渠道,一是直接证明结论的正确性,二是通过过程的正确性证明结论的正确性。第二种方法也可认为是演绎推理过程。如果每一步推理是正确的,结论必然正确。以用小棒摆平行为例,格尺的两边是平行的,小棒靠在格尺的两边来摆,小棒一定也是平行的。
在认识平行的过程中,教师要注意“变式”,由于我们在认识平行概念,所以“概念性变式”就显得很重要,有助于对概念的多角度理解。瑞典学者马顿为变式教学提供了理论基础,即“马顿理论”,以下被认为是马顿理论的核心:①学习就是鉴别(区分);②有比较(差异)才能鉴别。在认识平行过程中这几个反例是一定要让学生见到的:

(图—2)
(图—2)①标准变式,强化方向相同才平行;②强化直线的无限延展性;③是非标准变式,看似平行,其实是一条直线,强化两条或两条以上直线才出现平行;④强化直线延展性,有时平行是“用脑看出来的”;⑤“你能找出几组平行线?”渗透直线性质的传递性。
,