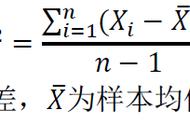由该表可知,由于 1 × 1 ≡ 1, 2 × 2 ≡ 1,所以 1 的逆元为 1, 2 的逆元为 2。也就是说,0 以外的数都有逆元,所以 {0, 1, 2} 构成了域。
4. 用 mod 4 进行分类则无法构成有限域接下来让我们用 (mod 4) 进行分类。剩余类共包含 0,1,2,3 这四类。

根据上表可知,此时 2 · 2 ≡ 0,所以 2 没有逆元。
也就是说,因为非 0 的 2 没有逆元,所以不能构成域。
5. 用 mod 5 进行分类时的有限域下面让我们来试试用 (mod 5) 进行分类。由于剩余类包含 0, 1,2,3,4,所以加法和乘法表如下。

根据乘法表可知,

由此可知,除 0 以外的其他“数”都有逆元。
6. 若 p 为素数,则剩余类为有限域至此,我们可以推测出当 n 为素数时,(mod n) 的剩余类能构成个数为 n 的有限域。
事实的确如此。
我们知道,当 p 为素数且用 (mod p) 进行分类时,费马小定理是成立的。
也就是说,对于非 0 的 a 而言,以下同余式恒成立。