In a floating-point representation, a value’s binary point is not fixed into a predefined position. That is, the interpretation of a binary sequence must encode how it’s representing the split between the whole and fractional parts of a value. While the position of the binary point could be encoded in many possible ways, this article focuses on just one, the Institute of Electrical and Electronics Engineers (IEEE) standard 754. Almost all modern hardware follows the IEEE 754 standard to represent floating-point values.
在浮点表示法中,值的二进制点不固定在预定义位置。也就是说,二进制序列的解释必须编码它如何表示一个值的整数部分和小数部分之间的分裂。虽然二进制点的位置可以通过多种可能的方式进行编码,但本文只关注其中一种,即电气和电子工程师协会(IEEE)标准754。几乎所有现代硬件都遵循IEEE 754标准来表示浮点值。

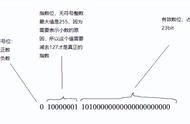
The 32-bit IEEE 754 floating-point standard
The above picture illustrates the IEEE 754 interpretation of a 32-bit floating-point number (C’s float type). The standard partitions the bits into three regions:
上图说明了32位浮点数(C的浮点类型)的IEEE 754解释。标准将位划分为三个区域:
1 The low-order 23 bits (digits through ) represent the significand (sometimes called the mantissa). As the largest region of bits, the significand serves as the foundation for the value, which ultimately gets altered by multiplying it according to the other bit regions. When interpreting the significand, its value implicitly follows a 1 and binary point.
1 低位23位(数字 至 )表示有效位(有时称为尾数)。作为最大的位区域,有效位用作值的基础,该值最终通过与其他位区域相乘而改变。解释有效位时,其值隐式跟随1和二进制点。
For example, if the bits of the significand contain 0b110000…0000, the first bit represents 0.5 (), the second bit represents 0.25 (), and all the remaining bits are zeros, so they don’t affect the value. Thus, the significand contributes 1.(0.5 0.25), or 1.75.
例如,如果尾数的位包含0b110000…0000,则第一位表示0.5 (),第二位表示0.25 (),所有剩余位均为零,因此它们不会影响值。因此,有效位表示1.(0.5 0.25)或1.75。
The next eight bits (digits through ) represent the exponent, which scales the significand’s value to provide a wide representable range. The significand gets multiplied by , where the 127 is a bias that enables the float to represent both very large and very small values.
接下来的八位((数字 至 )表示指数,它缩放尾数的值以提供一个宽阔的可表示范围。有效位乘以,其中127是一个偏差,使浮点既可以表示非常大的值,也可以表示非常小的值。
The final high-order bit (digit ) represents the sign bit, which encodes whether the value is positive (0) or negative (1).
最后一个高位(数字)表示符号位,它对值是正(0)还是负(1)进行编码。
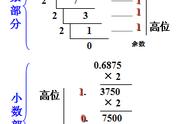
As an example, consider decoding the bit sequence 0b11000001101101000000000000000000. The significand portion is 01101000000000000000000, which represents = 0.40625, so the signifcand region contributes 1.40625. The exponent is 10000011, which represents the decimal value 131, so the exponent contributes a factor of. Finally, the sign bit is 1, so the sequence represents a negative value. Putting it all together, the bit sequence represents:
例如,考虑解码位序列0B110000011010000000000000000000000000。尾码部分为011000000000000000000000,表示= 0.40625,因此尾码部分表示1.40624。指数为1000011,表示十进制值131,因此指数表示的系数为。最后,符号位是1,因此序列表示负值。将其放在一起,位序列表示:
1.40625 × 16 × -1 = -22.5
While clearly more complex than the fixed-point scheme, the IEEE floating-point standard provides additional flexibility for representing a wide range of values. Despite the flexibility, a floating-point format with a constant number of bits still can’t precisely represent every possible value. That is, like fixed-point, rounding problems similarly affect floating-point encodings.
虽然IEEE浮点标准显然比定点方案更复杂,但它为表示宽范围的值提供了额外的灵活性。尽管具有灵活性,但具有恒定位数的浮点格式仍然不能精确表示所有可能的值。也就是说,与定点一样,舍入问题同样会影响浮点编码。
ref
Suzanne J. Matthews 《Dive into Systems》
https://diveintosystems.org/book/
-End-
,