大家好,我是站长 polarisxu。
团队一直保持着分享的习惯,而我却分享的较少。忘了当时同事分享什么主题,涉及到浮点数相关知识。于是我决定分享一期关于浮点数的,而且 Go 之父 Rob Pike 说不懂浮点数不配当码农。。。So?!

本着「要学习就系统透彻的学」这个原则,本文通过图的方式尽可能详细的讲解浮点数,让大家能够对浮点数有一个更深层次的认识。
本文目录:

开始之前请思考如下问题:
- 二进制 0.1,用十进制表示的话是多少?十进制的 0.1,用二进制表示又是多少?
- 为什么 0.1 0.2 = 0.30000000000000004?
- 单精度和双精度浮点数的有效小数位分别是多少?
- 单精度浮点数能表示的范围是什么?
- 浮点数为什么会存在 -0?infinity 和 NaN 又是怎么表示的?
如果现在不会,那这篇文章正好可以为你解惑。
1、什么是浮点数我们知道,数学中并没有浮点数的概念,虽然小数看起来像浮点数,但从不这么叫。那为什么计算机中不叫小数而叫浮点数呢?
因为资源的限制,数学中的小数无法直接在计算机中准确表示。为了更好地表示它,计算机科学家们发明了浮点数,这是对小数的近似表示。维基百科中关于浮点数的概念说明如下:
The term floating point refers to the fact that a number's radix point (decimal point, or, more commonly in computers, binary point) can float; that is, it can be placed anywhere relative to the significant digits of the number.
也就是说浮点数是相对于定点数而言的,表示小数点位置是浮动的。比如 7.5 × 10、0.75 × 10² 等表示法,值一样,但小数点位置不一样。
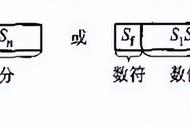
具体来说,浮点数是指用符号、尾数、基数和指数这四部分来表示的小数。

知道了浮点数的概念,但需要确定一套具体的表示、运算标准。其中最有名的就是 IEEE754 标准。William Kahan 正是因为浮点数标准化的工作获得了图灵奖。
The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point arithmetic established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found in the diverse floating-point implementations that made them difficult to use reliably and portably. Many hardware floating-point units use the IEEE 754 standard.
本文的讨论都基于 IEEE754 标准,这也是目前各大编程语言和硬件使用的标准。
根据上面浮点数的组成,因为是在计算机中表示浮点数,基数自然是 2,因此 IEEE754 浮点数只关注符号、尾数和指数三部分。
3、小数的二进制和十进制转换为了方便后面的内容顺利进行,复习下二进制和十进制的转换,其中主要涉及到小数的转换。
二进制转十进制和整数转换一样,采用各位数值和位权相乘。比如:
(0.101)₂ = 1×2⁻¹ 0×2⁻² 0×2⁻³ = (0.625)₁₀
记住小数点后第一位是从 -1 开始即可。
十进制转二进制十进制整数转二进制采用“除 2 取余,逆序排列”法。例如十进制数 11 转为二进制:
11/2=5…余1
5/2=2…余1
2/2=1…余0
1/2=0…余1
所以 (11)₁₀ 的二进制是 (1011)₂。
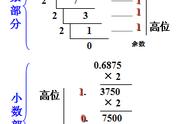
但如果十进制是小数,转为二进制小数如何做?采用“乘 2 取整,顺序排列”。例如十进制小数 0.625 转为二进制小数:
0.625*2=1.25…取整数部分1
0.25*2=0.5…取整数部分0
0.5*2=1…取整数部分1
顺序排列,所以 (0.625)₁₀ = (0.101)₂。
为了方便大家快速的做转换,网上有很多这样的工具。推荐一个我觉得最棒的:https://baseconvert.com/,支持各进制的转换,还支持浮点数。
4、经典问题:0.1 0.2 = 0.30000000000000004这个问题网上相关的讨论很多,甚至有专门的一个网站:https://0.30000000000000004.com/,这个网站上有各门语言的 0.1 0.2 的结果。比如 C 语言:
#include<stdio.h>
intmain(intargc,char**argv){
printf("%.17f\n",.1 .2);
return0;
}
Go 语言:
packagemain
import(
"fmt"
)
funcmain(){
vara,bfloat64=0.1,0.2
fmt.Println(a b)
}
结果都是 0.30000000000000004。
为什么会这样?这要回到 IEEE754 标准关于浮点数的规定。
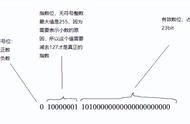
5、浮点数的 IEEE754 表示上文提到,浮点数由四个部分构成,那 IEEE754 标准是如何规定它们的存储方式的呢?
一般地,IEEE754 浮点数有两种类型:单精度浮点数(float)和双精度浮点数(double),还有其他的,不常用。单精度浮点数使用 4 字节表示;双精度浮点数使用 8 字节表示。在 Go 语言中用 float32 和 float64 表示这两种类型。