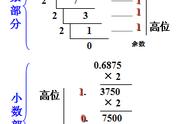
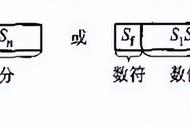
所以单精度浮点数的最大值应该能确认了,即:0 11111110 11111111111111111111111。

接着用问题的方式继续:单精度浮点数的最小值是多少(正数)?
根据前面的知识,我们会得到这样的最小值:0 00000000 00000000000000000000001。根据前面规范化浮点数的规定,我们知晓该值是:2⁻¹²⁷×(1 2⁻²³)。
然而,最小值的内存表示没错,但算出来的结果是错的。(额头冒汗没?怎么又错了~)
为了避免两个小浮点数相减结果是 0(也就是规范化浮点数无法表示)这样情况出现,同时根据规范化浮点数的定义,因为尾数部分有一个省略的前导 1,因此无法表示 0。所以,IEEE754 规定了另外一种浮点数:
当指数位全是 0,尾数部分不全为 0,尾数部分没有省略的前导 1,同时指数部分的偏移值比规范形式的偏移值小 1,即单精度是 -126,双精度是 -2046。这种形式的浮点数叫非规范化浮点数(denormal number)。
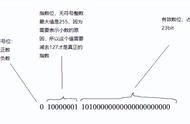
因此单精度浮点数的最小值(正数)如下图:

有了非规范化浮点数,IEEE754 就可以表示 0 了,但会存在 0 和 -0:即所有位全是 0 时是 0;符号位是 1,其他位是 0 时是 -0。
9、IEEE754 浮点数分类小结至此,浮点数相关的知识就介绍差不多了。为了让大家对整体再有一个更好的掌握,对浮点数的分类进行一些总结。
从上面的讲解,IEEE754 浮点数,指数是关键,根据指数,将其分为:特殊值、非规范化浮点数和规范化浮点数。

从上图规范化和非规范化浮点数的表示范围可以看出,两种类型的表示是具有连续性的。这也就是为什么非规范化浮点数指数规定为比规范形式的偏移值小 1(即单精度为 -126,双精度为 -2046)。
在数轴上,浮点数的分布: