引言
在计算机中,浮点数和定点数是常用的数值表示方法,用于处理和表示实数(包括小数)的数值。它们在计算机中具有不同的特点和应用场景。浮点数广泛应用于科学计算、金融计算等需要大范围和高精度的任务中。然而,浮点数在表示和计算过程中存在精度等问题。在接下来的介绍中,我们将探讨浮点数的内部表示、常见问题以及处理这些问题常用的解决方案。此外,本文还总结了一些通用的浮点数测试用例,希望可以帮助大家更好地理解和验证浮点数的精度特性。希望通过阅读本文,大家能对浮点数有更清晰的认识和应用。

浮点数的表示
浮点数在计算机内部表示中,小数点的位置是可变的,也就是说,小数点可以"浮动"在有效数字中的任意位置,因此得名。那么,在计算机表示中,它的小数点数如何“浮动”的呢,一起来看看浮点数是如何表示的。
最常用的浮点数表示方法是IEEE754,它是一种计算机浮点数算术标准,定义了浮点数的表示方法和浮点数运算规则。IEEE754标准规定了两种浮点数格式:单精度浮点数(32位)和双精度浮点数(64位),分别用于表示单精度和双精度实数。
十进制转二进制
首先,我们要知道常用的十进制,在二进制的计算机世界中是怎样的。
十进制的正数部分和小数部分转换为二进制的方法是不一样的,十进制整数转二进制使用的是除2取余数法,十进制小数转二进制用的是乘2取整法。
我们举例说明一下,以十进制数8.625为例:
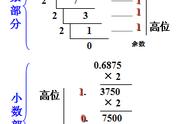
◆整数部分:将整数部分8转化为二进制,可以使用除2取余数法:
8除以2,商为4,余数为0,
将商4再次除以2,商为2,余数为0
将商2再次除以2,商为1,余数为0
将商1再次除以2,商为0,余数为1。
将以上得到的余数按倒序连接起来,得到整数部分的二进制表示为:1000
◆小数部分:将小数部分0.625转化为二进制,可以使用乘2取整法:
0.625 * 2 = 1.25,整数部分为1
剩余小数部分为0.25。0.25 * 2 = 0.5,整数部分为0
剩余小数部分为0.5。0.5 * 2 = 1.0,整数部分为1
剩余小数部分为0。
将以上得到的整数部分按顺序连接起来,得到小数部分的二进制表示为:101
综上,8.625的二进制表示为:1000.101
单精度浮点数
在IEEE 754 中单精度浮点数(32位)被拆成三个部分,分别是sign、exponent 跟fraction,加起来总共是32 个bit。下面以浮点数0.15625为例,看一下单精度浮点数的表示。
首先,需要将0.15625转化为二进制表示为0.00101,其规格化(类似于十进制科学计数法)表示为1.01 x 2^(-3)。
在分别看一下单精度浮点数三个部分的内容:
sign:即符号位,最左侧的1 bit 代表正负号,正数的话sign 就为0,反之则是 1
exponent:即阶码,中间的8 bit 代表规格化后的次方数,采用的是 超127格式,也就是-3 还要加上127 = 124,转化为二进制为1111100;整数前面补零不会影响整数的值,则不足8位时在前面补零,即为01111100。
fraction:即尾数,最右侧的23 bit 放的是小数部分,以1.01 来说就是去掉1. 之后的01。小数后面补零不影响小数的值,则尾数位不足23位在后面补零, 即为01000000000000000000000。
十进制数0.15625表示成单精度浮点数就如下图所示:

双精度浮点数
单精度浮点数只用了32 bit 来表示,为了让误差更小,提高精准度,IEEE 754 也定义了如何用64 bit 来表示浮点数,即双精度浮点数。跟32 bit 比起来尾数 部分大了超过两倍,从23 bit 变成52 bit,对比如下图所示: