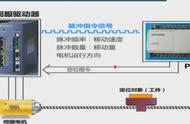
接下来我们来看一下这样一道题,它说是fx连续切,当x区域一的时候,函数的极限是等于上一个on的,然后要让我们求的是关于h的极限。
遇到这一类型题目的时候,很明显就是要利用倒数的定义来计算。什么是倒数的定义?常用的时候就是f在x0这一点处的导数就可以用极限形式把它表示出来,是不是就是do?x区域上一个x0的时候,函数的增量数fx减上一个fx零比上一个自变量的增量x减上一个x0,那么它的极限数就等于上一个它在x0这一点处的导数。
遇到这一类型的题的时候,首先是通过它告诉的极限求出,比如这是x区域一的,这样是相当于x0是不就等于上一个一,所以表示的就可以把它看成是不x是不是就是在等于一处的倒数的值,看能否把它凑出来,然后再把后面的处理写成倒数的形式来计算。

接下来就按照刚刚分析的思路来求解一下。首先把已知已知条件来推到它在一处的导数离比车,当x趋于一的时候,注意一下分子上是怎么样的了,分子上来看一下,稍等,看一下,注意到它是不是就是fx减上一个一,根据导数的定义,它是不是fx减上一个x0,分母上是不同样是为x减上一个x0,这样应该是x减上一个一。
但是会发现它这样是一个抛物线,pax商业派克斯为了凑这样的x减一就需要利用它的诱导公式。接下来来看一下,它说stary,需要一个是不是需要这样的x减一,就给它凑一个这样的,比如凑一个x减一,这样是x减一,这样是px,再给前面加上一个px,这样本身看一下,如果就是px减上一个p,本身只有一个px,所以这样还要加上一个px,加了一个减上一个π,还需要加上一个π,分子上是x,fx减上一个1是不变的。

再利用诱导公式,x区域一的时候处理一下,分母上的分子上是fx减上一个1,分母上是不在高中所要学习的是不机变偶不变,符号看象限配是不就是一个,是不是?所以它是一个偶数,它是不变的,所以是不就可以写成撒引数配乘上一个数x减一,这是不利用诱导公式。
·再来看一下,要出现x减一还是需要把撒引去掉,撒引如何去掉它?是不是就是利用近似替换,当x去零的时候数撒引x数近似与x,也就是这样把这样的x减一看算成一个整体x区域一的时候,这样的x减一是不是就是区域零配备的x减一仍然是区域零的,所以就直接可以把它近似而为配备的x减一。

·是不是就会发现这一部分不就是刚好是么?导数的定义,fx减f二一x减一,所以刚好是倒数的定义,所以这样就等于上一个。但是发现画红圈的这一部分表示的在一处的倒数,这个配分之一就可以放到前面去。
·但是会发现出现了一个错误,在利用诱导公式的时候是不是七变偶不变,光变了,但是符号没有看出来,符号开枪。现在说配加上一个角度,它说到第三象限,第三象限撒引是负的,所以这样插一个符号就可以得到这样的数据是一个符号。
·根据已知条件等于三个二,所以就可以推导出来在一处的导函数,算出来把负的配文直接移到右边去,就是负的昂派,这是在一处的导函数算出来了。
·接下来再来看一下要求的关于h的极限,也就是h去零的时候,看一下h区域零的时候分子上是不是就是一个平方差公式,平方差公式是不是就可以把它做一个英式分解,也就是f1加上一个h,然后加上一个fe减上一个h,这样是一个括号,在后面括号里面乘的时候就是f1加上一个h减上一个数,f1加上一个h,分母上数就是一个h。