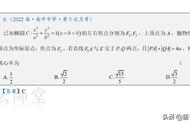
切线就是那个和曲线在某一点“刚好接触”的直线,而离心率就是描述圆锥曲线形状的一个参数。
切线是与曲线在某一点处只有一个公共点的直线。这意味着切线在这一点处与曲线“刚好接触”,而不会穿过曲线。切线的斜率等于曲线在该点处的导数。
求解切线方程的方法:首先,确定给定的点是否在曲线上。如果给定的点在曲线上,那么该点就是切点。如果给定的点不在曲线上,则需要通过其他方法找到切点。
接下来,求出该点处的导数,即切线斜率。导数可以通过对曲线方程进行求导得到。求出导数后,将切点的横坐标代入导数表达式,即可求出切线斜率。
最后,利用点斜式求出切线的方程。点斜式是一种用于求解直线方程的公式,它需要一个点和直线的斜率。在这个情况下,切点和切线斜率都已知,因此可以直接应用点斜式求出切线方程。
在求解切线问题时,需要注意以下几点:确认给定的点是否在曲线上;正确计算导数并求出切线斜率;根据题目要求,判断切线是否存在以及与曲线的位置关系。

离心率是描述圆锥曲线形状的一个重要参数。对于椭圆和双曲线,离心率分别定义为 c/a 和 c/b,其中 c 是焦点到中心的距离,a 和 b 分别是椭圆的长半轴和短半轴。对于抛物线,其离心率定义为 1。离心率的大小决定了圆锥曲线的形状和性质。
求解离心率的方法:首先,根据给定的圆锥曲线方程,确定 a、b 和 c 的值。这些值通常可以从方程中直接读出或通过简单的计算得到。然后,利用离心率的定义求出离心率。对于不同的圆锥曲线类型,离心率的计算方法也有所不同。例如,对于椭圆和双曲线,需要将 c、a 和 b 的值代入离心率的定义式进行计算;对于抛物线,则无需计算,因为其离心率恒为 1。
在求解离心率问题时,需要注意以下几点:准确识别圆锥曲线的类型;正确计算 a、b 和 c 的值;注意离心率与圆锥曲线形状之间的关系。不同的离心率值对应着不同的圆锥曲线形状和性质,因此在求解离心率问题时需要充分考虑这一点。
太原醍醐高补学校的老师让学生们在理解了基本概念后,会引导学生通过公式推导,掌握求解切线和离心率问题的方法。会将详细讲解求导法则和圆锥曲线的标准方程,让学生了解每一步的计算过程。
,