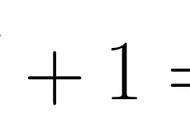这是指数函数和幂函数之间比较大小的问题。指数函数e^x中e>1,在R上无上界,单调递增。而幂函数x^2为标准二次函数,在正实数上也无上界且单调递增。

要比较这两个增函数,就要看二者增长的速度,我们可以通过图象来观察,易看到e^x的图象爆炸式增长,即e^ⅹ>x^2,如下图:

今天我要用数学归纳法来比较它们的大小。

由于是在正整数范围内比较二者大小,我们易知:
①当x=1时,e^ⅹ=e^1=e≈2.718,x^2=1^2=1,显然e^x>ⅹ^2 。
②当x=n时,不等式e^x>x^2成立,即有e^n>n^2。
③当x=n 1时,有e^(n 1)=e^nxe,而(n 1)^2=n^2 2n 1=n^2ⅹ(1 2/n 1/n^2)=n^2x(1 1/n)^2,
当n≥2时,(1 1/n)^2≤(1 1/2)^2=2.25<e,(当n=2时,1/n的最大值是1/2)。而由假设知e^n>n^2,
所以,当n≥2时,e^(n 1)=e^nXe>n^2X(1 1/n)^2=(n 1)^2,即e^(n 1)>n^2。
因此,由数学归纳法知,当X为正整数时,e^ⅹ>x^2恒成立。
事实上,数学归纳法是数学上常用的证明方法,在命题中出现正整数时,一般要考虑使用数学归纳法。