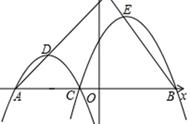
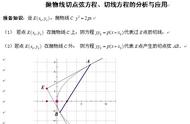
抛物线,作为数学中的一种重要曲线,具有许多令人惊叹的性质和特点。在这篇文章中,我们将深入探讨抛物线的八个二级结论,通过详细的讲解和引用相关书籍,带您领略抛物线的美妙之处。
一、焦点和准线的关系
抛物线的一个重要性质是,焦点到准线的距离等于准线上任意一点到曲线的距离。这一性质体现了抛物线的几何特点,可以通过几何推导和数学公式进行证明。

二、顶点的坐标
抛物线的顶点是其最高(或最低)点,对于一般形式的抛物线 $y = ax^2 bx c$,其顶点的横坐标为 $-\frac{b}{2a}$,纵坐标为 $-\frac{b^2 - 4ac}{4a}$。这个结论是通过数学分析和推导得出的。
三、对称轴的性质
抛物线关于其对称轴对称,因此对称轴是抛物线的一个重要特征。对于一般形式的抛物线 $y = ax^2 bx c$,其对称轴的方程为 $x = -\frac{b}{2a}$。
四、切线的斜率
在抛物线上任意一点处,切线的斜率等于该点的横坐标。这是一个有趣且有用的性质,可以通过微积分中的导数概念进行证明。

五、与坐标轴的交点
抛物线与坐标轴的交点是解其方程得到的。对于一般形式的抛物线 $y = ax^2 bx c$,与 x 轴的交点为 $(x_1, 0)$ 和 $(x_2, 0)$,其中 $x_1$ 和 $x_2$ 是方程 $ax^2 bx c = 0$ 的两个根。
六、拐点的存在
抛物线的拐点是其凹凸性发生变化的点,对于一般形式的抛物线 $y = ax^2 bx c$,拐点的横坐标为 $-\frac{b}{2a}$,纵坐标为 $-\frac{1}{4a}$。这个结论可以通过对抛物线的二阶导数进行分析得出。

七、极值点的性质
抛物线在其顶点处达到最大值或最小值,这也是极值点的性质。对于一般形式的抛物线 $y = ax^2 bx c$,当 $a > 0$ 时,抛物线开口向上,顶点是极小值点;当 $a < 0$ 时,抛物线开口向下,顶点是极大值点。
八、与直线的关系
抛物线与直线的交点数量有限,可能有两个、一个或零个交点。交点的数量取决于抛物线与直线的位置关系和方程的系数。

引用数学经典著作
如果您对抛物线和曲线的性质感兴趣,可以阅读一些相关的数学经典著作。《微积分学教程》(托马斯,引自《微积分学教程》)是一本深入浅出地讲解微积分概念和应用的书籍,或许会为您深入理解抛物线的性质提供帮助。
通过本文的讲解,我们可以更全面地了解抛物线的八个二级结论,以及这些结论背后的数学原理。抛物线作为数学中的重要曲线,不仅具有美丽的几何特点,还具有丰富的应用价值。希望您能在探索抛物线的世界中,更加深入地领略数学的魅力和奥妙。