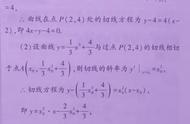导数可以说是研究函数行为最有用的数学工具。
在这篇文章中,我们将介绍计算机计算导数的三种方法。
为了简单起见,我们将只讨论单变量函数。但是,同样的概念也适用于处理多元函数。
导数是什么?
函数的导数表示函数值随参数的微小变化而变化的速率。
我们定义一个函数f(x)在点x0处的导数:

视觉上,f(x)的导数是:任意x0切线的斜率:


应用这个定义,我们可以找到简单函数导数的一般表达式,如多项式、指数、三角函数等。
因此,我们推出了两种计算导数的方法:
通过某一点x₀,根据定义
利用已知函数的导数表达式和链式法则
下面,我们将从计算的角度探讨每种方法
数值微分
如前面所述,第一种方法意味着使用有限差分法计算某个点x₀处近似导数的值:
为了实现这个方法,我们选择一个小的h(接近于零)计算分数