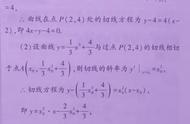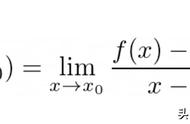高考数学新题型——新定义:平方弯曲度,利用导数研究斜率,巧用均值定理和换元法求最值。

本题给出了平方弯曲度的概念:在一个函数上存在不同的两个点,在这两点处的切线的斜率是KA和KB,定义KA-KB的绝对值比上AB的平方为平方弯曲度。

我们就要借助导数的几何意义来求KA和KB并借助两点间的距离公式求出AB的平方。
大家看一下图,给出的曲线y=ex x且x1-x2=1,这个式子求解太麻烦了,我们根据式子特点发现,借助换元法,将双变量问题转化为单变量问题,巧用基本不等式(均值定理)求解一次比二次分式型函数的最值问题。
本题得分率仅有0.1,难就难在计算上,换元法是解题的关键。换元法一定要注意三个关键:易做性、彻底性和等价性。

如需系统学习请查看高考数学总复习专栏,详见目录,20天一栏通关高考数学总复习,祝大家高考成功。

如需系统学习请留言。
以下为新高一使用:
按住“点赞”3秒留言领取免费配套资源。
,