三角内插法是一种常用的数值计算方法,主要用于求解一元函数的值。它通过构造一个简单的三角形来逼近给定的函数,从而得到函数在某个点的近似值。这种方法具有简单、易理解和计算方便的优点,因此在科学计算、工程技术和经济分析等领域得到了广泛的应用。
一、三角内插法的基本原理
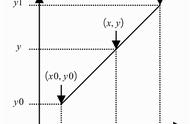
三角内插法的基本原理是通过构造一个简单的三角形来逼近给定的函数。假设我们要求解函数f(x)在点x0处的值,首先需要构造一个以x0为顶点的三角形。这个三角形的两个基点可以取为x0的左右邻域内的两个点x1和x2,其中x1
具体来说,三角内插法的公式为:
f(x0)≈f(x1) x−xf(x)−f(x)⋅(x0−x1)
其中,x1和x2是构造三角形时选取的两个基点,而f(x1)、f(x2)和f(x0)分别是这三个点的函数值。
二、三角内插法的应用
三角内插法具有广泛的应用,下面列举几个常见的应用场景:
1、数据拟合:在数据分析和统计中,经常需要对数据进行拟合,以找到最佳的函数模型。三角内插法可以用于构造一个简单的三角形来逼近给定的数据点,从而得到最佳的拟合效果。
2、数值积分:在数值积分中,三角内插法可以用于计算定积分的近似值。通过构造一个以积分区间端点为顶点的三角形,可以计算出积分的近似值。
3、优化问题:在优化问题中,三角内插法可以用于求解一些简单的约束优化问题。通过构造一个以最优解为顶点的三角形,可以找到最优解的近似值。
4、插值问题:在数学和工程中,经常需要求解一些函数的插值问题。三角内插法可以用于构造一个简单的三角形来逼近给定的函数,从而得到函数的近似值。
5、经济分析:在经济分析中,三角内插法可以用于求解一些简单的经济模型。通过构造一个以经济变量为顶点的三角形,可以计算出经济变量的近似值。
三、三角内插法的优缺点
三角内插法具有以下优点:
1、简单易理解:三角内插法是一种直观的方法,其基本原理简单易懂,容易掌握。
2、计算方便:三角内插法的计算过程相对简单,易于实现。
3、应用广泛:三角内插法在许多领域都有广泛的应用,如数据拟合、数值积分、优化问题、插值问题和经济分析等。
然而,三角内插法也存在一些缺点:
1、精度较低:由于三角内插法是通过构造一个简单的三角形来逼近给定的函数,其精度受到三角形形状的影响,可能无法得到高精度的结果。
2、不适用于复杂函数:对于一些复杂的函数,三角内插法的逼近效果可能不够理想,因为三角形只能近似表示简单的函数形状。
3、对噪声敏感:如果数据中含有噪声,三角内插法的结果可能会受到较大的影响,因为噪声可能会改变三角形顶点的位置和形状。
四、总结
本文介绍了三角内插法的基本原理、应用和优缺点。作为一种简单易懂的数值计算方法,三角内插法在许多领域都有广泛的应用。然而,由于其精度较低、不适合复杂函数以及容易受到噪声影响等缺点,在实际应用中需要注意其适用范围和限制条件。未来可以通过改进三角内插法的算法和提高其精度等方法,进一步拓展其应用范围和发挥其优势。
,