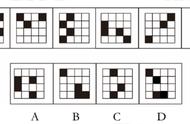
一.概念描述
现代数学:一般地说,变换是指某个集合中符合一定要求的一种对应规律。就图形的变换来讲,因为几何图形都是点的集合,所以图形变换可以通过点的变换来实现。如果一个平面图形的每一个点,都对应于该平面内某个新图形的一个点,并且新图形中的每一个点只对应于原图形中的一个点,这样的对应就叫图形变换。几何变换中最重要的是全等变换与相似变换。
小学数学:在小学数学教材中没有对图形变换给出明确的定义。但对图形变换中最重要的两种变换形式---全等变换和相似变换都有所涉及。如小学阶段的全等变换主要学习了平移变换、旋转变换和轴对称变换;在六年级学习比例尺后,学习图形的放大和缩小,实际上就是一种相似变换。
二.概念解读
几何图形都是点的集合,所以图形变换可以通过点的变化来实现。图形在变换过程中,平面图形上的每一个点,与同一平面内某个新图形的每个点都对应,并且新图形中的每个点只对应于原图形中的一个点。
图形在变换过程中有两种形式, 一种图形变换前后图形的形状和大小不变,仅仅是位置变化,这种变换称为全等变换。在全等变换中,原图形任何两点之间的距离,都等于新图形中两对应点之间的距离,所以全等变换又称为保距变换。
全等变换有几种变化方式。我们可以直观地想象一下,形状、大小一样的两个图形,其中的一个图形可以通过怎样的“运动”与另一个图形重合。
下面我们以两个全等的三角形为例---把其中的一个三角形平移到另一个三角形,当两个三角形其中的一个顶点能够重合时,会出现几种情况呢?
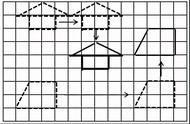
第一种:这两个三角形完全重合了。(如下图)

第二种:两个三角形没能完全重合,但通过绕这个顶点旋转一定的角度就能完全重合。(如下图)

第三种:两个三角形没能完全重合,通过绕这个顶点旋转一定的角度还不能完全重合,此时还需要经过图形的翻转才能使两个三角形完全重合。(如下图)

从上面的例子不难看出,这三种情况其实就是三种基本的全等变换,即平移变换、旋转变换、轴对称变换(反射变换)。
图形变换的另一种形式,就是形状不变但大小发生了变化,这种变换称为相似变换。相似变换能够保持图形的形状不变,而只改变图形的大小。在相似变换中,原图形中所有角的大小都保持不变,所以相似变换又称为保角变换。
三.教学建议
在小学数学教学中,对于图形变换主要学习了三种基本的全等变换,也就是平移变换、旋转变换和轴对称变换。相似变换只是在第二学段中有所渗透,如学习比例尺时两个图形按比例放大或缩小,实际上就是一种相似变换。因此,教学中教师要认识到这些变换的相同与不同,准确把握小学阶段的具体要求。
(1)教学时要在具体情境中引导学生认识变换现象
学生很早就有了物体或图形运动的经验,他们通过折纸、玩风车、照镜子等生活经验,早已获得了诸如平移、旋转、反射等体验。因此,教学中教师要善于调动学生的这些生活经验,为学生提供大量的丰富的运动现象,给学生充分的想象时间和空间,鼓励学生对这些素材加以分析,从而直观认识变换现象。
(2)教学中要通过观察、操作、分类等活动体会变换的特征
学生在直观认识变换现象后,教师还需要引导学生通过观察、操作、分类等一系列的活动,从整体感受变换现象到初步感受变换特征进而初步刻画变换特征的过程。
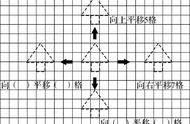
例如,在学生对平移变换有了初步认识后,一般在小学三年级,教材都会安排学生尝试在方格纸上面出一个图形经过变换后的图形,如下图。

学生在解决这一问题时,是存在一些问题的,如有的学生在找平移格数时认为两棵小树中间空的格子就是平移的格数,此时,教师可以借助动画演示,引导学生观察发现,平移前后对应点的距离是相等的,进而感受到可以借助点的距离来确定平移的距离。实际上,这样的活动正是让学生在整体感受变换现象的基础上,尝试如何刻画平移,当然这个过程是借助方格纸并通过操作实现的。
又如,在小学六年级学生学习完比例尺后,研究两个图形按比例放大或缩小这一内容时,教师可以尝试这样设计教学:①从生活中的放大,缩小引入,让学生感受到生活中存在许多放大与缩小的现象,进而引出研究问题---“图形的放大与缩小”。②为学生提供必要的学具
(方格纸、直尺),组织学生探索交流放大或缩小后的图形与原图比较有什么发现?
在交流中使学生初步感受到把一个图形的各边按一定的比例可以进行放大或缩小,从而得到该图形放大或缩小后的图形。在探索中,学生会发现放大或缩小后的图形长和宽的比与原来图形的长和宽的比是完全一样的。但教师要认识到,此时对于“放大或缩小”的学习不是相似变换的学习,主要是直观感知,即放大或缩小后的图形与原图形形状相同、大小不同。这样的探索过程为学生今后研究相似变换奠定了基础。
四.推荐阅读
《小学数学教学策略》(张丹,北京师范大学出版社,2010)
该书第170-179页针对图形与变换的教学提出了一些具体的教学策略。文章还有很多案例分析,对于案例的分析解读也很精彩。
,