设所求平面的方程为Ax+By+Cz+D=0,其法向量为n=(A,B,C)≠0,即A,B和C不全为0.
首先讨论A,B和C这3个数中有一个数为0时的情形:
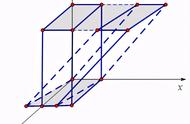
(1)若A=0,则n在x轴上的投影为0,从而所求平面的法向量与x轴垂直,所求平面与x轴平行;反之,若所求平面与x轴平行,则所求平面的法向量与x轴垂直,从而在x轴上的投影为0,因此可设所求平面的方程为By+Cz+D=0.同理可知,如果B=0,则所求平面的方程可设为Ax+Cz+D=0;如果C=0,则所求平面的方程可设为Ax+By+D=0. 如下图所示∶

A=0时的情形

B=0时的情形

C=0时的情形
(2)如果A=B=0,则n⫽k,从而平面π与xOy面平行,从而所求平面的方程可设为Cz D=0. 由C≠0可知,z=-C/D,因此平面方程可设为z=k.
同理可知,如果B=C=0,则所求平面与yOz面平行,因此所求平面的方程可设为x=d;如果A=C=0,则所求平面与xOz面平行,因此所求平面的方程可设为y=h.(这里的k,d,h都是常数.)如下图所示∶

A=B=0时的情形

B=C=0时的情形

A=C=0时的情形
,