原创 林根数学 林根数学 昨天
仿射变换的一个特点,就是“平直性”,因为我们可以理解仿射变换是一个线性变换加上一个平移,线性这个性质就保证了直线变换后还是直线,所以仿射变换,变换后的图形,是直线边的还是直线边。
介绍下面两种特殊的线性变换:
错切变换:错切变换是一种特殊的“平直性”变换,简单来说就是矩形变为平行四边形,长方体变为平行六面体,如下图:

反之平行六面体通过错切变换也可以变成长方体。
压缩变换:平面压缩变换是由x’=nx , y’=my,给出, 其中n 、m 为正数。若取n = 1, 则称变换x’=x 、y’= my为向着ox轴的压缩变换(下面谈到的变换都是指这种压缩变换)。
被压缩的图形叫做原像, 压缩变换成的图形叫做像。
显然,错切变换和压缩变换有下面几个基本不变性质:
1 .两条平行(重合) 或相交的直线在压缩变换下的像也是平行(重合) 或相交的直线;
2. 在压缩变换下,同一直线上或平行线段的比值仍保持不变.
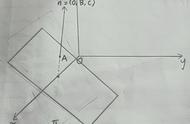
至于在空间坐标系中,空间三点的平面方程的求法,用行列式比较方便:
求过三点:M₁(x₁, y₁,z₁);M₂(x₂,y₂,z₂);M₃(x₃,y₃,z₃)的平面的方法:
设过M₁的平面方程为A(x-x₁) B(y-y₁) C(z-z₁)=0.................①
M₂,M₃都在此平面上,因此它们的坐标都满足方程①;将它们的坐标依次代入得:
A(x₂-x₁) B(y₂-y₁) C(z₂-z₁)=0.............②
A(x₃-x₁) B(y₃-y₁) C(z₃-z₁)=0..............③
①②③是关于A、B、C的线性方程组,此方程组有非零解的充要条件是关于A、B、C的系数行列式∆=0;即:

下面由此来看,2020年人大附中的一道期中考试压轴题:
人大附中2020-2021 学年度第一学期高二年级数学期中练习20201104 第24 题
已知四棱锥T - ABCD的底面为平行四边形,平面α与直线 AD,TA,TC分别交于点P,Q,R ,且

点M 在直线TB 上, N 为CD的中点,且直线MN∥平面α.
(1)设