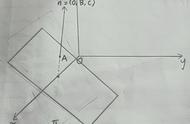
试用基底

表示向量TD;
(2)证明:四面体TABC 中至少存在一个顶点,从其出发的三条棱能够组成一个三角形;
(3)证明:对所有满足条件的平面α,点M 都落在某一条长为(√5/2)TB 的线段上.
证明:前两问极容易,属于可以“秒*”的情形,这里从略.
(3) 把四棱锥T – ABCD嵌入如图1所示的平行六面体中,沿Ox轴及Oy轴作两次错切变换得到长方体,再作一次压缩变换得到一正方体(棱长为1),上述变换中原题设的定比分点的比不变,所求结论中的比值√5/2亦不变.

如图2所示,在正方体ABCD-A’B’C’T中解决问题即可.

可设P(0,1-x,0), Q(0, x,1-x), R (1-x , 0,x),过此三点的平面α方程为