最近进入备考攻坚期,建议大家回归基础内容。近期也有考生反映,题和公式对不上,或是不懂公式的意思。这其实是因为在记忆公式时忘记把概念一起理解记忆,从而导致看不懂题意。今天我们就来再复习成考数学部分基础内容:
集合及简易逻辑1、交集:集合 A 与集合 B 的交集记作 A∩B,取 A、B 两集合的公共元素(阴影部分)

2、并集:集合 A 与集合 B 的并集记作 A∪B,取 A、B 两集合的全部元素(全部阴影部分)

3、补 集:已知全集 U,集合 A 的补集记作CUA,取 U 中所有不属于 A 的元素(阴影部分)

集合一般是选择题常出现的一个题型,相对比较简单,大家务必要掌握。如果搞不清这三者关系,可以结合图示记忆。

一个数学命题会有条件和结论两部分,如果把条件和结论分别用A、B表示,那么命题可以写成“如果A成立,那么B成立”,或简写成“若A,则B”。
如果A成立,那么B成立,即A→B,这时我们说条件A是B成立的充分条件
如果B成立,那么A成立,即A←B,这时我们说条件A是B成立的必要条件
如果A既是B成立的充分条件,又是B成立的必要条件,即既有A→B,又有B→A,这时我们说条件A是B成立的充分必要条件,简称充要条件。
要判断一个命题的条件是结论成立的什么条件,首先要分清楚命题的“条件”、“结论”,设它们分别为P,Q。然后再检查是否有P→Q成立,或Q→P成立.

直线:(不定义)直线向两方无限延伸,它无端点。
射线:在直线上某一点旁的部分。射线只有一个端点。
线段:直线上两点间的部分。它有两个端点。
垂线:如果两条直线相交成直角,那么称这两条直线互相垂直。其中一条叫另一条的垂线,它们的交点叫垂足。
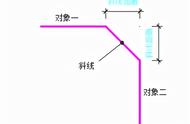
斜线:如果两条直线不相交成直角时,其中一条直线叫另一条直线的斜线。点到直线的距离从直线外一点到这条直线的垂线段的长度,叫做点到直线距离。
平面内两点的距离公式:已知P1(x1,y1);P2(x2,y2)两点,其距离:|P1P2|=√[(x1-x2)2 (y1-y2)2]
线段的中点公式:已知已知P1(x1,y1);P2(x2,y2)两点,线段P1P2的中点M的坐标为(X,Y),则:x=(x1 x2)/2;y=(y1 y2)/2
直线斜率的定义为k=tanα(α为倾斜角),已知两点可以求的斜率k=(y2-y1)/(x2-x1);(点A(x1,y1)和点B(x2,y2)为直线上任意两点)。

点斜式:y-y0=k(x-x0);已知斜率k和某点坐标(x0,y0)
斜截式:y=kx b;已知斜率k和在y轴的截距b
两点式:(y-y1)/(y2-y1)=(x-x1)/(x2-x1),已知两点坐标A(x1,y1);B(x2,y2)
截距式:x/a y/b=1,已知在x轴的截距式a,在y轴的截距式b
一般式:Ax By C=0
备考时间所剩无几,务必把宝贵时间用到刀刃上,多研究常考的、易于掌握的内容。考试科目里也要选择自己相对擅长的科目作为拿分项,毕竟成考不看单科看总分。
提醒大家,对于语文这项“必争科目”,更要好好冲刺备考,尤其是其中占比大的作文题!
,