学习目标
1.证据推理与模型认知:构建盖斯定律模型,理解盖斯定律的本质,形成运用盖斯定律进行 相关判断或计算的思维模型。
2.科学态度与社会责任:了解盖斯定律对反应热测定的重要意义,增强为人类科学发展而努 力的意识与社会责任感
知识导学
知识点 1 盖斯定律
1.盖斯定律的内容 大量实验证明,一个化学反应,不管是一步完成的还是分几步完成的,其反应热是相同的。 换句话说,化学反应的反应热只与反应体系的始态和终态有关,而与反应的途径无关。
2.盖斯定律的意义 应用盖斯定律可以间接计算以下情况(不能直接测定)的反应热:
(1)有些反应进行得很慢。
(2)有些反应不容易直接发生。
(3)有些反应的生成物不纯(有副反应发生)。
3.应用盖斯定律的计算方法
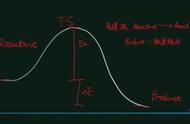
(1)“虚拟路径”法 若反应物 A 变为生成物 D,可以有两个途径
①由 A 直接变成 D,反应热为ΔH;
②由 A 经过 B 变成 C,再由 C 变成 D,每步的反应热分别为ΔH1、ΔH2、ΔH3。 如图所示:

则有ΔH=ΔH1+ΔH2+ΔH3。
(2)加合法 加合法就是运用所给热化学方程式通过加减乘除的方法得到所求的热化学方程式。

举例说明: 根据如下两个反应,选用上述两种方法,计算出 C(s)+ 1 2 O2(g)===CO(g)的反应热ΔH。
Ⅰ.C(s)+O2(g)===CO2(g) ΔH1=-393.5 kJ·mol-1
Ⅱ.CO(g)+ 1 2 O2(g)===CO2(g) ΔH2=-283.0 kJ·mol-1
①“虚拟路径”法 反应 C(s)+O2(g)====CO2(g)的途径可设计如下

则ΔH=ΔH1-ΔH2=-110.5 kJ·mol
②加合法 分析:找唯一:C、CO 分别在Ⅰ、Ⅱ中出现一次 同侧加:C 是Ⅰ中反应物,为同侧,则“+Ⅰ” 异侧减:CO 是Ⅱ中反应物,为异侧,则“-Ⅱ” 调计量数:化学计量数相同,不用调整,则Ⅰ-Ⅱ即为运算式。所以ΔH=ΔH1-ΔH2=-110.5 kJ· mol-1。
例 1.已知反应: H2(g)+ 1 2 O2(g)===H2O(g) ΔH1 1 2 N2(g)+O2(g)===NO2(g) ΔH2 1 2 N2(g)+ 3 2 H2(g)===NH3(g) ΔH3 则反应 2NH3(g)+ 7 2 O2(g)===2NO2(g)+3H2O(g)的ΔH 为( )
A.2ΔH1+2ΔH2-2ΔH3
B.ΔH1+ΔH2-ΔH3
C.3ΔH1+2ΔH2+2ΔH3
D.3ΔH1+2ΔH2-2ΔH3
例 2.根据下列热化学方程式: ①C(s)+O2(g)===CO2(g) ΔH1=-393.5 kJ·mol-1 ②H2(g)+ 1 2 O2(g)===H2O(l) ΔH2=-285.8 kJ·mol-1 ③CH3COOH(l)+2O2(g)===2CO2(g)+2H2O(l) ΔH3=-870.3 kJ·mol-1 可以计算出 2C(s)+2H2(g)+O2(g)====CH3COOH(l)的反应热为________________(写出计算 过程)。
知识点 2 反应热的计算
1.根据热化学方程式计算 热化学方程式中反应热数值与各物质的化学计量数成正比。例如,