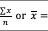在统计函数的第八讲中,我们进一步讲了RANK函数计算名次位置的统计方法,统计函数在数据处理中有着很重要的地位,一段时间以来我已经就各个函数进行了详细的讲解,今日将讲最后的一集,中位数。这个函数在我之前也是讲解过的,在统计函数的讲解中,我仍单独作为一节来讲解,作为统计函数的最后的一节。
MEDIAN函数定义: 返回给定数值集合的中值.中值是在一组数据中居于中间的数,即在这组数据中,有一半的数据比它大,有一半的数据比它小。
使用格式:
MEDIAN(Number1,number2,...)。
格式简义:MEDIAN(单元格或单元格区域)。
参数定义:Number 要计算中值的1到30个数值。
注意事项:
a)参数应为数字,或者是包含数字的名称、数组或引用。MicrosoftExcel会检查每一数组参数或引用中的所有数字。
b).如果数组或引用参数包含文本、逻辑值或空白单元格,则这些值将被忽略;但包含零值的单元格将计算在内。
c).如果参数集合中包含偶数个数字,函数MEDIAN将返回位于中间的两个数的平均值。
d)中位数:就是数值按顺序排序时,正好居中的数值。所求的中位数范围是偶数时,处于中央位置的数值就有两个,此时居中的两个数值的平均值就为中位数。
e)几个定义:
①平均值:平均值是算术平均数,由一组数相加然后除以这些数的个数计算得出。例如2、3、3、5、7 和 10 的平均数是 30 除以 6,结果是 5。
②中位数: 中值是一组数中间位置的数;即一半数的值比中值大,另一半数的值比中值小。例如,2、3、3、5、7 和 10 的中值是 4。
③众数:众数是一组数中最常出现的数。例如,2、3、3、5、7 和 10 的众数是 3。
④对于对称分布的一组数来说,这三种趋中性计算方法是相同的。对于偏态分布的一组数来说,这三种趋中性计算方法可能不同。
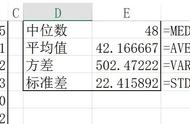
对于这个函数是比较好理解的,通过我上面的讲解是很容易掌握的。最后我们再看下面的截图会更好的理解这个函数:

在第一行中,中位数左右对称后中间的数是2,故中位数是2;在第四行中中间是2和3,所以中位数是2加3的平均数是2.5。
统计函数共讲了九讲,到这里就全部讲完了,以后或者有机会在其他的文章中还会涉及到。到时候再和大家分享。
今日内容回向:
1 MEDIAN函数的意义是什么?
2中位数、众数、平均数的区别是什么?
,