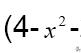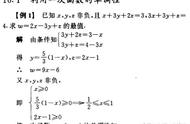以下是高等数学的一条定理,作为了解,可以快速求极大值与极小值

补充:怎么求二阶导数,简单的说一下,对于高中知识来说,最简单的做法就是先求一次导,再对此导数再求一次导就是二阶导数了。
对以上试题f'(x)=x²-4=(x-2)(x+2)
f'(x)=0,f(x)在x1=-2,x2=2处有二阶导数,f''(x)=2x≠0(把x1,x2代入可知)
则f"(-2)=-4<0,故函数f(x)在x1=-2处取得极大值
f"(2)=4>0,函数f(x)在x=2处取得极小值
此方法作用快速确定极大极小值,作为验证可以用,在高中数学中以高中知识求即可。涉及的内容比较多,在此就不在赘述。由于篇幅较长,后会对其知识点准备高考试题进行巩固。
最后总结,求函数极值步骤:
①求函数导数
②求函数导数零点
③画表格,定义域分区间(一般以导数零点作为分区间讨论),导数,原函数之间的关系
④确定极值(若左边导数大于零,右边导数小于零,在此取得极大值,反之是极小值)
由于水平有限,若有不当之处请指出,欢迎大家一起探讨。以下附上一般函数的求导及函数求导方法: