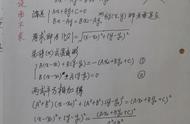大家好,我是前端西瓜哥。
今天来实现计算两条线段的交点的解析几何算法。
我们要实现 getLineSegIntersection 方法:提供两条线段,计算它们的交点。
每条线段会用两个点坐标表示。
constgetLineSegIntersection=(p1,p2,p3,p4)=>{
//待实现
}
//测试用例
getLineSegIntersection(
{x:1,y:1},{x:4,y:4},
{x:1,y:4},{x:4,y:1}
);
//期望{x:2.5,y:2.5}
思路
思路很简单,就是解两条直线对应的一个二元一次方程组,求出 x 和 y。
如果无解或多解,说明直线平行,交点不存在。
如果有解,可拿到唯一交点,但也只能说明直线有交点,还需要判断线段是否有交点。
所以我们需要判断交点是否在线段的区间上。如果是,说明两线段有交点,返回交点。
克拉姆法则解方程组需要用到 克拉姆法则。
对于:

可转换为矩阵形式表示:

然后计算主矩阵(最左边的矩阵)的行列式,对角相乘然后相减:

如果行列式为 0,说明没有唯一解;
如果不为 0,则有唯一解:

回到我们的两条直线,我们用两点式表示直线:

转换成 Ax By=C 的格式,得到:

于是:
consta=y2-y1;
constb=x1-x2;
constc=x1*y2-x2*y1;
第二条线段同理:
constd=y4-y3;
conste=x3-x4;
constf=x3*y4-x4*y3;
算法实现
interfacePoint{
x:number;
y:number;
}
constgetLineSegIntersection=(
p1:Point,
p2:Point,
p3:Point,
p4:Point
):Point|null=>{
const{x:x1,y:y1}=p1;
const{x:x2,y:y2}=p2;
const{x:x3,y:y3}=p3;
const{x:x4,y:y4}=p4;
consta=y2-y1;
constb=x1-x2;
constc=x1*y2-x2*y1;
constd=y4-y3;
conste=x3-x4;
constf=x3*y4-x4*y3;
//计算分母
constdenominator=a*e-b*d;
//判断分母是否为0(代表平行)
if(Math.abs(denominator)<0.000000001){
//这里有个特殊的重叠但只有一个交点的情况,可以考虑处理一下
returnnull;
}
constpx=(c*e-f*b)/denominator;
constpy=(a*f-c*d)/denominator;
//判断交点是否在两个线段上
if(
px>=Math.min(x1,x2)&&
px<=Math.max(x1,x2)&&
py>=Math.min(y1,y2)&&
py<=Math.max(y1,y2)&&
px>=Math.min(x3,x4)&&
px<=Math.max(x3,x4)&&
py>=Math.min(y3,y4)&&
py<=Math.max(y3,y4)
){
return{x:px,y:py};
}
returnnull;
};
变体
这个算法可以做一些变体,实现其他的算法。
变体1:两线段是否有交点。
返回值换成布尔值即可。
判断两线段是否有交点,我之前还写了另一种解法,感兴趣可以看看:
《几何算法:判断两条线段是否相交》
变体2:计算两直线的交点。
把判断直线交点是否在线段上的逻辑去掉,然后直接返回点坐标即可。
优化点1、重叠但却只有一个交点的情况。
如果线段平行,有两种情况:
- 没有重叠(0 个解)
- 有部分重叠(多解)
如果部分重叠,可能有多个点,多个点的情况下也不知道拿哪个点作为交点好,这种情况下还是返回 null。
但有一个特殊的情况:重叠只有一个点(比如线段 a 的末点刚好是线段 b 的起点)。如果你的场景下判断比较严格,你可以选择返回这个点。要实现这部分也是有点点复杂的。
2、误差处理。线段的两个端点的距离非常小,计算出的结果也会非常小,可能会进入了 0 的绝对误差范围了,考虑改成相对误差。
3、溢出风险。数值很大时有溢出风险,可以考虑计算一个缩放值,缩小后计算,计算完再放大回去。
结尾总结一下,求两线段的交点,本质就是解方程,需要用到克莱姆法则,计算出来的交点是直线交点,不一定是线段交点,需要再判断点是否在线段范围内。
不复杂,就是有一点点小细节。
我是前端西瓜哥,欢迎关注我,学习更多解析几何知识。
,