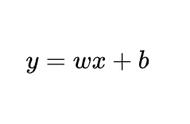,其中α为学习率
3.如何选取α,如何停止更新权值
a.通常α取0.001,根据实验结果依次增加三倍,比较实验结果。0.001,0.003,0.01,0.03,0.1 b.θ更新到什么时候停止?每次更新后,带入θ值可以求得J(θ)的值,比较当前的J(θ)与上一次的值,如果变化很小,则可认为达到收敛;或者不断增加迭代次数,可视化观察J(θ)的曲线图。
4.正则化
使用L1范数(权值为非0的权值和)称为Lasso回归,使用L2范数(权值平方和)称为岭回归。正则化项称为惩罚函数,目的解决过拟合问题,代价函数变为:

这里使用的是L2范数,J(θ)称为岭回归
二、逻辑回归1.概念
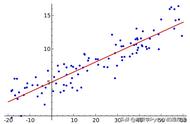
逻辑回归由线性回归转变而来,线性回归用来预测具体的值,如果遇到分类问题如何解决呢?这里还是使用线性回归来拟合数据,然后再对其预测值进行0 1 映射(使用sigmod函数),因此得到的逻辑回归模型为:

sigmod函数就是形式S形状的函数,存在上限、下限
2.代价函数
这里可以均方误差作为代价函数,但是图像非凸函数,使用梯度下降很难求得其收敛值,因此这里借助于极大似然估计的概念来设计逻辑回归的代价函数:对于二分类:
X01概率1-pp
似然函数:

对数形式: